解:(1)∵∠AFB=150°,∴∠OFB=30°(O为坐标原点)
在直角△BOF中,|FB|=2|OB|,∴a=2b
∵点A(-2,0)在椭圆
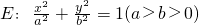
上,∴a=2,∴b=1
∴椭圆
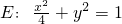
;
(2)∵直线l过x轴上一点M(m,0)(m≠-2)不垂直于y轴,∴l:x=ty+m
与椭圆方程联立
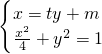
,消元整理可得(t
2+4)y
2+2mty+m
2-4=0
∴△=4m
2t
2-4(t
2+4)(m
2-4)>0,∴t
2>m
2-4
设C(x
1,y
1),D(x
2,y
2),∴
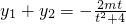
,
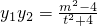
(i)若以CD为直径的圆恒过A点,则
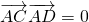
∵

=(x
1+2,y
1),

=(x
2+2,y
2),
∴x
1x
2+2(x
1+x
2)+4+y
1y
2=

∴
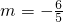
或m=-2(舍去)
∴实数m的值为

;
(ii)若△ACD的重心恒在y轴的左侧,即重心的横坐标恒小于0,即
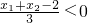
,∴
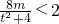
∴4m<t
2+4对所有符合条件的t恒成立
由t
2>m
2-4知:
①若m
2-4<0,即-2<m<2时,t
2∈[0,+∞),∴t
2+4≥4,∴m<1,∴-2<m<1;
②若m
2-4≥0,即m≤-2或m≥2时,t
2∈(m
2-4,+∞),∴4m<m
2,∴m≤0或m≥4
综上知,实数m的取值范围是(-∞,-2)∪(-2,1)∪[4,+∞).
分析:(1)根据∠AFB=150°,可得∠OFB=30°(O为坐标原点),从而可知a=2b,又a=2,故可求椭圆E的方程;
(2)根据直线l过x轴上一点M(m,0)(m≠-2)不垂直于y轴,假设l:x=ty+m与椭圆方程联立
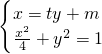
,消元整理可得(t
2+4)y
2+2mty+m
2-4=0,利用△=4m
2t
2-4(t
2+4)(m
2-4)>0,可得t
2>m
2-4
(i)若以CD为直径的圆恒过A点,利用
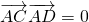
,可求实数m的值;
(ii)若△ACD的重心恒在y轴的左侧,即重心的横坐标恒小于0,,结合t
2>m
2-4,分类讨论,即可求得实数m的取值范围.
点评:本题考查椭圆的标准方程,考查直线与椭圆的位置关系,考查分类讨论的数学思想,解题的关键是直线方程与椭圆方程联立,利用韦达定理解题.

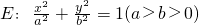 上,设椭圆E与y轴正半轴的交点为B,其左焦点为F,且∠AFB=150°.
上,设椭圆E与y轴正半轴的交点为B,其左焦点为F,且∠AFB=150°.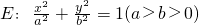 上,∴a=2,∴b=1
上,∴a=2,∴b=1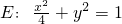 ;
;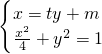 ,消元整理可得(t2+4)y2+2mty+m2-4=0
,消元整理可得(t2+4)y2+2mty+m2-4=0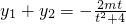 ,
,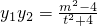
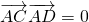
 =(x1+2,y1),
=(x1+2,y1), =(x2+2,y2),
=(x2+2,y2),
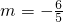 或m=-2(舍去)
或m=-2(舍去) ;
;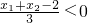 ,∴
,∴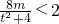
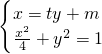 ,消元整理可得(t2+4)y2+2mty+m2-4=0,利用△=4m2t2-4(t2+4)(m2-4)>0,可得t2>m2-4
,消元整理可得(t2+4)y2+2mty+m2-4=0,利用△=4m2t2-4(t2+4)(m2-4)>0,可得t2>m2-4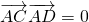 ,可求实数m的值;
,可求实数m的值;

 名校课堂系列答案
名校课堂系列答案