
分析 (1)化为分段函数,画出图象即可;
(2)由图象得到函数的单调区间;
(3)由图象求出最值.
解答 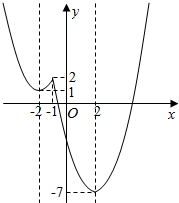 解:(1)$f(x)=\left\{\begin{array}{l}{x^2}-4x-3(x≥-1)\\{x^2}+4x+5(x<-1)\end{array}\right.$=$\left\{\begin{array}{l}{(x-2)^2}-7(x≥-1)\\{(x+2)^2}+1(x<-1)\end{array}\right.$,(2分)
解:(1)$f(x)=\left\{\begin{array}{l}{x^2}-4x-3(x≥-1)\\{x^2}+4x+5(x<-1)\end{array}\right.$=$\left\{\begin{array}{l}{(x-2)^2}-7(x≥-1)\\{(x+2)^2}+1(x<-1)\end{array}\right.$,(2分)
其图象如右图所示. (6分)
(2)f(x)的单调减区间为(-∞,-2),(-1,2);
单调增区间为(-2,-1),(2,+∞)(10分)
(3)由图象知,当x=2时,f(x)取得最小值-7.(12分)
点评 本题考查了函数图象的画法和识别,以及函数的单调性,最值,属于基础题.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:高中数学 来源: 题型:选择题
| A. | (1)、(2) | B. | (1)、(3) | C. | (1)、(4) | D. | (3)、(4) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
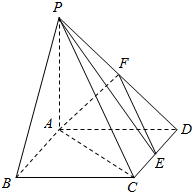 如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,且PA=AD,点F是棱PD的中点,点E在棱CD上移动.求证:PE⊥AF.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,且PA=AD,点F是棱PD的中点,点E在棱CD上移动.求证:PE⊥AF.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知函数f(x)=x2-2$|\begin{array}{l}{x}\end{array}|$
已知函数f(x)=x2-2$|\begin{array}{l}{x}\end{array}|$查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 关于直线x=$\frac{π}{6}$对称 | B. | 关于直线x=$\frac{π}{4}$对称. | ||
| C. | 关于点($\frac{π}{4}$,0)对称 | D. | 关于点($\frac{π}{6}$,0)对称 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com