
(本题满分10分,其中第1小题5分,第二小题5分)
规定含污物体的清洁度为:![]() 。现对1个单位质量的含污物体进行清洗,清洗前其清洁度为0.8,要求洗完后的清洁度是0.99。有两种方案可供选择,方案甲:一次清洗;方案乙:两次清洗。该物体初次清洗后受残留水等因素影响,其质量变为a(1≤a≤3)。设用x单位质量的水初次清洗后的清洁度是
。现对1个单位质量的含污物体进行清洗,清洗前其清洁度为0.8,要求洗完后的清洁度是0.99。有两种方案可供选择,方案甲:一次清洗;方案乙:两次清洗。该物体初次清洗后受残留水等因素影响,其质量变为a(1≤a≤3)。设用x单位质量的水初次清洗后的清洁度是![]() (
(![]() ),用y质量的水第二次清洗后的清洁度是
),用y质量的水第二次清洗后的清洁度是![]() ,其中c(
,其中c(![]() )是该物体初次清洗后的清洁度。
)是该物体初次清洗后的清洁度。
(Ⅰ)分别求出方案甲以及![]() 时方案乙的用水量,并比较哪一种方案用水量较少;
时方案乙的用水量,并比较哪一种方案用水量较少;
(Ⅱ)若采用方案乙,当a为某定值时,如何安排初次与第二次清洗的用水量,使总用水量最少?并讨论a取不同数值时对最少总用水量多少的影响。
科目:高中数学 来源: 题型:
(2009江苏卷)(本题满分10分)
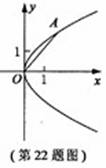 在平面直角坐标系
在平面直角坐标系![]() 中,抛物线C的顶点在原点,经过点A(2,2),其焦点F在
中,抛物线C的顶点在原点,经过点A(2,2),其焦点F在![]() 轴上。
轴上。
(1)求抛物线C的标准方程;
(2)求过点F,且与直线OA垂直的直线的方程;
(3)设过点![]() 的直线交抛物线C于D、E两点,ME=2DM,记D和E两点间的距离为
的直线交抛物线C于D、E两点,ME=2DM,记D和E两点间的距离为![]() ,求
,求![]() 关于
关于![]() 的表达式。
的表达式。
查看答案和解析>>
科目:高中数学 来源: 题型:
(2009江苏卷)(本题满分10分)
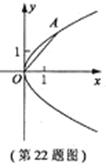
在平面直角坐标系![]() 中,抛物线C的顶点在原点,经过点A(2,2),其焦点F在
中,抛物线C的顶点在原点,经过点A(2,2),其焦点F在![]() 轴上。
轴上。
(1)求抛物线C的标准方程;
(2)求过点F,且与直线OA垂直的直线的方程;
(3)设过点![]() 的直线交抛物线C于D、E两点,ME=2DM,记D和E两点间的距离为
的直线交抛物线C于D、E两点,ME=2DM,记D和E两点间的距离为![]() ,求
,求![]() 关于
关于![]() 的表达式。
的表达式。
查看答案和解析>>
科目:高中数学 来源:2013届湖北省仙桃市高二下学期期中考试理科数学试卷(解析版) 题型:解答题
(本题满分10分)
设函数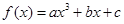
 为奇函数,其图象在点
为奇函数,其图象在点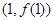 处的切线与直线
处的切线与直线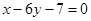 垂直,导函数
垂直,导函数 的最小值为
的最小值为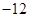 .试求
.试求 ,
,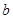 ,
,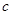 的值。
的值。
查看答案和解析>>
科目:高中数学 来源:2013届福建省高二下学期期中考试文科数学试卷(解析版) 题型:解答题
(本题满分10分)
已知一个算法如下:
S1 输入X;
S2 若X<0,执行S3;否则,执行S5;
S3  ;
;
S4 输出Y,结束;
S5 若X=0,执行S6;否则执行S8;
S6  ;
;
S7 输出Y,结束;
S8  ;
;
S9 输出Y,结束.
(1)指出其功能(用数学表达式表示);
(2)请将该算法用程序框图来描述之.
查看答案和解析>>
科目:高中数学 来源:2012届甘肃省高三9月月考理科数学试卷 题型:解答题
(本题满分10分) 若向量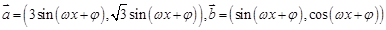 ,其中
,其中 ,设
,设
函数 ,其周期为
,其周期为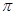 ,且
,且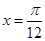 是它的一条对称轴。
是它的一条对称轴。
(1)求 的解析式;
的解析式;
(2)当 时,不等式
时,不等式 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com