
(14分)如图,已知四棱锥 的正视图和侧视图均是直角三角形,俯视图为矩形,N、F分别是SC、AB的中点,
的正视图和侧视图均是直角三角形,俯视图为矩形,N、F分别是SC、AB的中点,  ,
,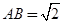 .
.
(1)求证:SA⊥平面ABCD
(2)求证:NF∥平面SAD;
(3)求二面角A-BN-C的余弦值.
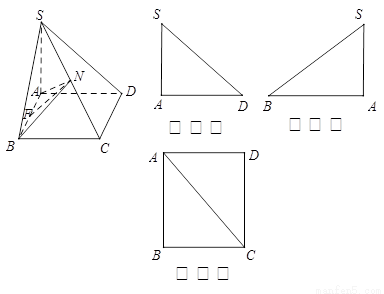
17. (1)∵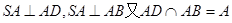 ∴
∴ -------(3分)
-------(3分)
(2)取SD的中点N,连接MN,AM
∵N为SC的中点,∴MN∥CD且MN=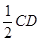
又矩形ABCD中,F为AB的中点,∴AF∥CD且AF=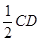
∴AF∥MN且AF=MN 则四边形AFNM为平行四边形----------(5分)
∴AM∥FN
AM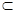 平面SAD FN
平面SAD FN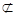 平面SAD
∴NF∥平面SAD------(7分)
平面SAD
∴NF∥平面SAD------(7分)
(3)以 点为原点,
点为原点,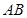 所在直线为
所在直线为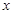 轴,
轴,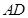 所在直线为
所在直线为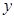 轴,SA所在直线为
轴,SA所在直线为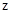 轴的空间直角坐标系,如图所示.
轴的空间直角坐标系,如图所示.
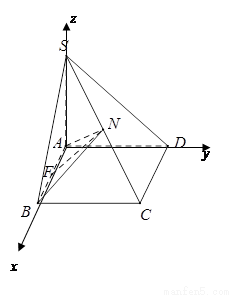
则依题意可知相关各点的坐标分别是:
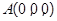 ,
,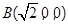 ,
,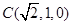 ,
,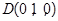 ,
,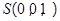 如下图所示.
如下图所示.
∴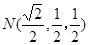 ------------------…(9分)
------------------…(9分)
∴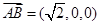 ,
,
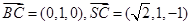 --------------(10分)
--------------(10分)
设平面ABN的法向量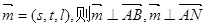

令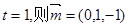 ----------------------------------------(11分)
----------------------------------------(11分)
设平面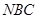 的法向量
的法向量 ,则
,则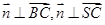 ,
,
所以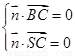 即
即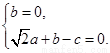
所以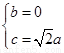
令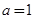 ,则
,则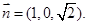 ------------------------------ (12分)
------------------------------ (12分)
∴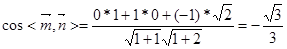 ------------ (13分)
------------ (13分)
由图形知,二面角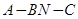 是钝角二面角
是钝角二面角
所以二面角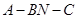 的余弦值为
的余弦值为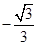 ......................................................... (14分)
......................................................... (14分)
【解析】略


 习题精选系列答案
习题精选系列答案科目:高中数学 来源: 题型:
 如图,已知正四棱柱ABCD-A1B1C1D1,点E在棱D1D上,截面EAC∥D1B,且面EAC与底面ABCD所成的角为45°,AB=a.
如图,已知正四棱柱ABCD-A1B1C1D1,点E在棱D1D上,截面EAC∥D1B,且面EAC与底面ABCD所成的角为45°,AB=a.查看答案和解析>>
科目:高中数学 来源: 题型:
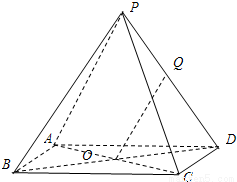
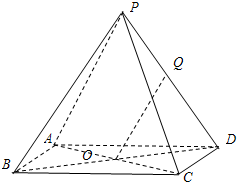 (2007•静安区一模)(理) 如图,已知四棱锥P-ABCD的底面ABCD是边长为a的正方形,点O为该正方形的中心,侧棱PA=PC,PB=PD.
(2007•静安区一模)(理) 如图,已知四棱锥P-ABCD的底面ABCD是边长为a的正方形,点O为该正方形的中心,侧棱PA=PC,PB=PD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
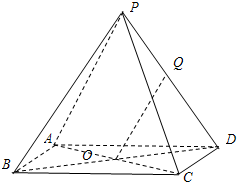 (理) 如图,已知四棱锥P-ABCD的底面ABCD是边长为a的正方形,点O为该正方形的中心,侧棱PA=PC,PB=PD.
(理) 如图,已知四棱锥P-ABCD的底面ABCD是边长为a的正方形,点O为该正方形的中心,侧棱PA=PC,PB=PD.查看答案和解析>>
科目:高中数学 来源:2008年上海市静安区高考数学一模试卷(文理合卷)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com