
 )cos(x+
)cos(x+ )的图象中,相邻两个对称中心的距离为π;
)的图象中,相邻两个对称中心的距离为π; 对称,则
对称,则 ;
;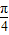 )cos(x+
)cos(x+ )=
)=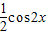 ,能求出在它的图象中相邻两个对称中心的距离;②由函数y=log2|3x-m|的图象关于直线x=
,能求出在它的图象中相邻两个对称中心的距离;②由函数y=log2|3x-m|的图象关于直线x= 对称,知log2|3x-m|=log2|3(1-x)-m|,由此能求出m;③关于x的方程ax2-2x+1=0有且仅有一个实数根,则实数a=1,或a=0;④已知命题p:?x∈R,都有sinx≤1,则¬p是:?x∈R,使得sinx>1.
对称,知log2|3x-m|=log2|3(1-x)-m|,由此能求出m;③关于x的方程ax2-2x+1=0有且仅有一个实数根,则实数a=1,或a=0;④已知命题p:?x∈R,都有sinx≤1,则¬p是:?x∈R,使得sinx>1.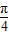 )cos(x+
)cos(x+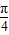 )=sin(x+
)=sin(x+ )cos(x+
)cos(x+ )=
)=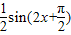 =
=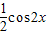 ,
, ,故①不正确;
,故①不正确; 对称,
对称, ,故②正确;
,故②正确;

 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案科目:高中数学 来源: 题型:
| a |
| b |
| a |
| b |
查看答案和解析>>
科目:高中数学 来源:北京市石景山区2006-2007学年度高三年级第一学期期末统一考试、数学(理科) 题型:022
对于函数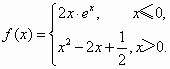 有下列命题:
有下列命题:
①过该函数图像上一点(-2,f(-2))的切线的斜率为![]() ;
;
②函数f(x)的最小值为![]() ;
;
③该函数图像与![]() 轴有4个交点;
轴有4个交点;
④函数f(x)在(-∞,-1]上为减函数,在(0,1]上也为减函数.
其中正确命题的序号是________
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| a |
| b |
| a |
| b |
| A.0 | B.1 | C.2 | D.3 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年山东省枣庄市高三(上)期中数学试卷(理科)(解析版) 题型:选择题
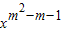 的图象不过原点,则m=l或2;
的图象不过原点,则m=l或2;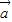 =(t,2),
=(t,2), =(-3,6),若向量
=(-3,6),若向量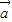 与
与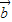 的夹角为锐角,则实数t的取值范围是t<4;
的夹角为锐角,则实数t的取值范围是t<4; 查看答案和解析>>
科目:高中数学 来源:2012-2013学年山东省枣庄市高三(上)期中数学试卷(理科)(解析版) 题型:选择题
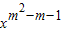 的图象不过原点,则m=l或2;
的图象不过原点,则m=l或2;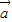 =(t,2),
=(t,2),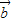 =(-3,6),若向量
=(-3,6),若向量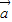 与
与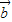 的夹角为锐角,则实数t的取值范围是t<4;
的夹角为锐角,则实数t的取值范围是t<4; 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com