
【题目】已知焦点在![]() 轴上的椭圆
轴上的椭圆![]() 上的点到两个焦点的距离和为10,椭圆
上的点到两个焦点的距离和为10,椭圆![]() 经过点
经过点![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)过椭圆![]() 的右焦点
的右焦点![]() 作与
作与![]() 轴垂直的直线
轴垂直的直线![]() ,直线
,直线![]() 上存在
上存在![]() 、
、![]() 两点满足
两点满足![]() ,求△
,求△![]() 面积的最小值;
面积的最小值;
(3)若与![]() 轴不垂直的直线
轴不垂直的直线![]() 交椭圆
交椭圆![]() 于
于![]() 、
、![]() 两点,交
两点,交![]() 轴于定点
轴于定点![]() ,线段
,线段![]() 的垂直平分线交
的垂直平分线交![]() 轴于点
轴于点![]() ,且
,且![]() 为定值,求点
为定值,求点![]() 的坐标.
的坐标.
科目:高中数学 来源: 题型:
【题目】政府工作报告指出,2018年我国深入实施创新驱动发展战略,创新能力和效率进一步提升;2019年要提升科技支撑能力,健全以企业为主体的产学研一体化创新机制.某企业为了提升行业核心竞争力,逐渐加大了科技投入;该企业连续6年来的科技投入![]() (百万元)与收益
(百万元)与收益![]() (百万元)的数据统计如下:
(百万元)的数据统计如下:
科技投入 | 2 | 4 | 6 | 8 | 10 | 12 |
收益 |
|
|
|
|
|
|
根据散点图的特点,甲认为样本点分布在指数曲线![]() 的周围,据此他对数据进行了一些初步处理,如下表:
的周围,据此他对数据进行了一些初步处理,如下表:
|
|
|
|
|
|
|
|
|
|
|
|
其中![]() ,
,![]() .
.
(1)(i)请根据表中数据,建立![]() 关于
关于![]() 的回归方程(保留一位小数);
的回归方程(保留一位小数);
(ii)根据所建立的回归方程,若该企业想在下一年的收益达到2亿,则科技投入的费用至少要多少(其中![]() )?
)?
(2)乙认为样本点分布在二次曲线![]() 的周围,并计算得回归方程为
的周围,并计算得回归方程为![]() ,以及该回归模型的相关指数
,以及该回归模型的相关指数![]() ,试比较甲、乙两位员工所建立的模型,谁的拟合效果更好.
,试比较甲、乙两位员工所建立的模型,谁的拟合效果更好.
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线方程
,其回归直线方程![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为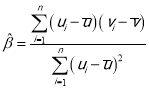 ,
,![]() ,相关指数:
,相关指数: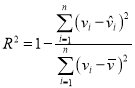 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】工人在安装一个正六边形零件时,需要固定如图所示的六个位置的螺丝,第一阶段,首先随意拧一个螺丝,接着拧它对角线上(距离它最远的,下同)螺丝,再随意拧第三个螺丝,第四个也拧它对角线上螺丝,第五个和第六个以此类推,但每个螺丝都不要拧死;第二阶段,将每个螺丝拧死,但不能连续拧相邻的2个螺丝.则不同的固定方式有________.
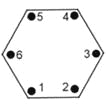
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三棱锥P-ABC(如图1)的展开图如图2,其中四边形ABCD为边长等于![]() 的正方形,△ABE和△BCF均为正三角形,在三棱锥P-ABC中.
的正方形,△ABE和△BCF均为正三角形,在三棱锥P-ABC中.
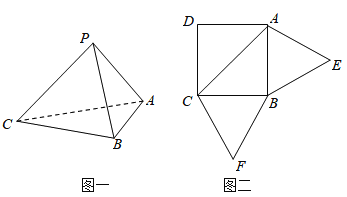
(1)证明:平面PAC⊥平面ABC;
(2)若M,N分别是AP,BC的中点,请判断三棱锥M-BCP和三棱锥N-APC体积的大小关系并加以证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设![]() 为曲线
为曲线![]() 上的点,
上的点,![]() ,垂足为
,垂足为![]() ,若
,若![]() 的最小值为
的最小值为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com