
【题目】定义函数f(x)=(1﹣x2)(x2+bx+c).
(1)如果f(x)的图象关于x=2对称,求2b+c的值;
(2)若x∈[﹣1,1],记|f(x)|的最大值为M(b,c),当b、c变化时,求M(b,c)的最小值.
【答案】(1)-1(2)![]() .
.
【解析】
(1)由![]() 的图象关于直线
的图象关于直线![]() 对称,则将
对称,则将![]() 的图象向左移动
的图象向左移动![]() 个单位,得到函数
个单位,得到函数![]() 为偶函数,化简,由偶函数性质即可得出结论.
为偶函数,化简,由偶函数性质即可得出结论.
(2) 由任意![]() 记
记![]() 的最大值为
的最大值为![]()
取![]() ,
,![]() 得
得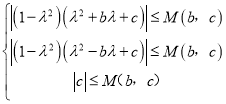 ,
,
化简可得![]() ,只需要
,只需要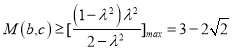 ,即可求出
,即可求出![]() 的最小值.
的最小值.
.
(1)f(x)的图象关于直线x=2对称,则将f(x)的图象向左移动2个单位,得到函数,
g(x)=f(x+2)=[1﹣(x+2)2][(x+2)2+b(x+2)+c]=﹣x4﹣(8+b)x3﹣(19+4b)x2﹣(28+11b+4c)x﹣(12+6b+3c)为偶函数,
∴![]() 解得
解得![]() ,
,
∴2b+c=﹣1;
(2)对任意的x∈[﹣1,1],|f(x)|≤M(b,c),
取x=±λ得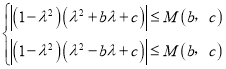 ,
,
同理取x=0得,|c|≤M(b,c),
由上述三式得:2|(1﹣λ2)(λ2+c)|≤2M(b,c),
∴|(1﹣λ2)(λ2+c)|≤M(b,c),
∴|(1﹣λ2)λ2|≤|(1﹣λ2)(λ2+c)|+|(1﹣λ2)|c||≤(2﹣λ2)M(b,c),
因此,M(b,c)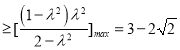 (当且仅当λ2=2
(当且仅当λ2=2![]() 时,取得最大值),此时b=0,c
时,取得最大值),此时b=0,c![]() ,
,
经验证,![]() 满足题意.
满足题意.
故当b=0,c![]() 时,M(b,c)取得最小值,且最小值为
时,M(b,c)取得最小值,且最小值为![]() .
.


 走进文言文系列答案
走进文言文系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 过点
过点 ,且离心率为
,且离心率为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若点![]() 与点
与点![]() 均在椭圆
均在椭圆![]() 上,且
上,且![]() 关于原点对称,问:椭圆上是否存在点
关于原点对称,问:椭圆上是否存在点![]() (点
(点![]() 在一象限),使得
在一象限),使得![]() 为等边三角形?若存在,求出点
为等边三角形?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大型歌手选秀活动,过程分为初赛、复赛和决赛.经初赛进入复赛的40名选手被平均分成甲、乙两个班,由组委会聘请两位导师各负责一个班进行声乐培训.下图是根据这40名选手参加复赛时获得的100名大众评审的支持票数制成的茎叶图.赛制规定:参加复赛的40名选手中,获得的支持票数不低于85票的可进入决赛,其中票数不低于95票的选手在决赛时拥有“优先挑战权”.
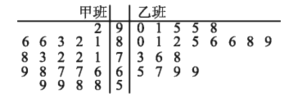
(1)从进入决赛的选手中随机抽出2名,X表示其中拥有“优先挑战权”的人数,求X的分布列和数学期望;
(2)请填写下面的![]() 列联表,并判断能否在犯错误的概率不超过0.025的前提下认为进入决赛与选择的导师有关?
列联表,并判断能否在犯错误的概率不超过0.025的前提下认为进入决赛与选择的导师有关?
甲班 | 乙班 | 合计 | |
进入决赛 | |||
未进入决赛 | |||
合计 |
下面的临界值表仅供参考:
P( | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式: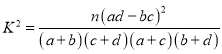 ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex﹣2mx﹣n(0<x<1),其中m,n∈R,e为自然对数的底数.
(1)试讨论函数f(x)的极值;
(2)记函数g(x)=ex﹣mx2﹣nx﹣1(0<x<1),且g(x)的图象在点![]() 处的切的斜率为
处的切的斜率为![]() ,若函数g(x)存在零点,试求实数m的取值范围.
,若函数g(x)存在零点,试求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为更好进行校纪、校风管理,争创文明学校,由志愿者组成“小红帽”监督岗,对全校的不文明行为进行监督管理,对有不文明行为者进行批评教育,并作详细的登记,以便跟踪调查下表是![]() 个周内不文明行为人次统计数据:
个周内不文明行为人次统计数据:
周次 |
|
|
|
|
|
不文明行为人次 |
|
|
|
|
|
(1)请利用所给数据求不文明人次![]() 与周次
与周次![]() 之间的回归直线方程
之间的回归直线方程![]() ,并预测该学校第
,并预测该学校第![]() 周的不文明人次;
周的不文明人次;
(2)从第![]() 周到第
周到第![]() 周记录得知,高一年级有
周记录得知,高一年级有![]() 位同学,高二年级有
位同学,高二年级有![]() 位同学已经有
位同学已经有![]() 次不文明行为.学校德育处决定先从这
次不文明行为.学校德育处决定先从这![]() 人中任选
人中任选![]() 人进行重点教育,求抽到的两人恰好来自同一年级的概率
人进行重点教育,求抽到的两人恰好来自同一年级的概率
参考公式: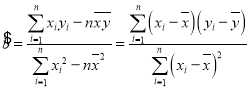 ,
,![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com