
【题目】已知点![]() 和向量
和向量![]()
(1)若向量![]() 与向量
与向量![]() 同向,且
同向,且![]() ,求点
,求点![]() 的坐标;
的坐标;
(2)若向量![]() 与向量
与向量![]() 的夹角是钝角,求实数
的夹角是钝角,求实数![]() 的取值范围.
的取值范围.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】从某小区抽取100户居民进行月用电量调查,发现其用电量都在50至350度之间,频率分布直方图如图所示: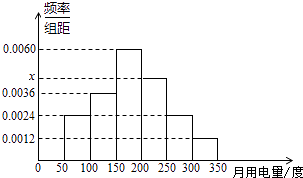
(Ⅰ)直方图中x的值为;
(Ⅱ)在这些用户中,用电量落在区间[100,250)内的户数为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等比数列{an}的公比为q,记bn=am(n﹣1)+1+am(n﹣1)+2+…+am(n﹣1)+m , cn=am(n﹣1)+1am(n﹣1)+2…am(n﹣1)+m , (m,n∈N*),则以下结论一定正确的是( )
A.数列{bn}为等差数列,公差为qm
B.数列{bn}为等比数列,公比为q2m
C.数列{cn}为等比数列,公比为 ![]()
D.数列{cn}为等比数列,公比为 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 年北京市进行人口抽样调查,随机抽取了某区居民
年北京市进行人口抽样调查,随机抽取了某区居民![]() 人,记录他们的年龄,将数据分成
人,记录他们的年龄,将数据分成![]() 组:
组:![]() ,
,![]() ,
,![]() ,…
,…![]() ,并整理得到如下频率分布直方图:
,并整理得到如下频率分布直方图:

(Ⅰ)从该区中随机抽取一人,估计其年龄不小于![]() 的概率;
的概率;
(Ⅱ)估计该区居民年龄的中位数(精确到![]() );
);
(Ⅲ)假设同组中的每个数据用该组区间的中点值代替,估计该区居民的平均年龄.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱柱ABCD﹣A1B1C1D1中,侧棱AA1⊥底面ABCD,AB∥DC,AA1=1,AB=3k,AD=4k,BC=5k,DC=6k,(k>0)
(1)求证:CD⊥平面ADD1A1
(2)若直线AA1与平面AB1C所成角的正弦值为 ![]() ,求k的值
,求k的值
(3)现将与四棱柱ABCD﹣A1B1C1D1形状和大小完全相同的两个四棱柱拼成一个新的四棱柱,规定:若拼成的新四棱柱形状和大小完全相同,则视为同一种拼接方案,问共有几种不同的拼接方案?在这些拼接成的新四棱柱中,记其中最小的表面积为f(k),写出f(k)的解析式.(直接写出答案,不必说明理由)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,O是坐标原点,两定点A,B满足| ![]() |=|
|=| ![]() |=
|= ![]()
![]() =2,则点集{P|
=2,则点集{P| ![]() =λ
=λ ![]() +μ
+μ ![]() ,|λ|+|μ|≤1,λ,μ∈R}所表示的区域的面积是( )
,|λ|+|μ|≤1,λ,μ∈R}所表示的区域的面积是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com