
 在xoy平面上有一系列点P1(x1,y1),P2(x2,y2),…,Pn(xn,yn),…,对每个正整数n,以点Pn为圆心的⊙Pn与x轴及射线y=
在xoy平面上有一系列点P1(x1,y1),P2(x2,y2),…,Pn(xn,yn),…,对每个正整数n,以点Pn为圆心的⊙Pn与x轴及射线y=| 3 |
| xnan-1 |
| xn+an-1 |
| 5 |
| 4 |
| 1 |
| 3n-1 |
| ||
(1-
|
| ||
(1-
|
| ||
(1-
|
| 4 |
| 5 |
| 1 | ||||
1+an+
|
| (xn-xn+1)2+(yn-yn+1)2 |
|
| ||
| 3 |
| xnan-1 |
| xn+an-1 |
| 2 |
| 3n-1 |
| 2 |
| 8 |
| 1 |
| 3 |
| 2 |
| 26 |
| 1 |
| 9 |
| 2 |
| 3n-1 |
| 1 |
| 3n-1 |
(1-an)2
| ||
(1-
|
(1-an)2
| ||
(1-
|
(1-ak)2
| ||
(1-
|
| ||||
(1+ak+
|
| ||
| 3 |
| xn | ||
|
| (xn-xn+1)2+(yn-yn+1)2 |
|
| ||
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| xnan-1 |
| xn+an-1 |
| 1 |
| an |
| 1 |
| xn |
| 1 |
| an-1 |
| 1 |
| an |
| 1 |
| an-1 |
| 1 |
| xn |
| 1 |
| an |
| 1 |
| a1 |
| 1 |
| x2 |
| 1 |
| x3 |
| 1 |
| xn |
| 1 |
| an |
| 1 |
| x2 |
| 1 |
| x3 |
| 1 |
| xn |
| 3n-1 |
| 2 |
| 2 |
| 3n-1 |
| 5 |
| 4 |
| 1 |
| 3n-1 |
| 2 |
| 8 |
| 1 |
| 3 |
| 2 |
| 26 |
| 1 |
| 9 |
| 2 |
| 3n-1 |
| 1 |
| 3n-1 |
| 1 |
| 12 |
| 13 |
| 12 |
| 5 |
| 4 |
| 1 |
| 32-1 |
| 9 |
| 8 |
| 2 |
| (3n-1)3n-1 |
| 2 |
| (3n-1)(3n-1-1) |
| 2•3n-1 |
| (3n-1)(3n-1-1) |
| 1 |
| 3n-1-1 |
| 1 |
| 3n-1 |
| 1 |
| 12 |
| 1 |
| 32-1 |
| 1 |
| 33-1 |
| 1 |
| 33-1 |
| 1 |
| 34-1 |
| 1 |
| 3n-1-1 |
| 1 |
| 3n-1 |
| 1 |
| 12 |
| 1 |
| 8 |
| 1 |
| 3n-1 |
| 29 |
| 24 |
| 1 |
| 3n-1 |
| 5 |
| 4 |
| 1 |
| 3n-1 |
| 1 |
| an |
| 1 |
| an-1 |
| 1 |
| xn |
(1-an)2
| ||
(1-
|
(1-an)2
| ||
(1-
|
(1-ak)2
| ||
(1-
|
| ||||
(1+ak+
|
| ||||||||||
(1+ak+
|
| 1 | ||||
1+ak+
|
| 1 | ||||||
1+ak+
|
| 1 | ||||
1+ak+
|
| 1 | ||||||
1+ak+1+
|
| 1 | |||||
|
| 1 | |||||
|
| 2 |
| 32-1 |
| 1 |
| 4 |
| ||
(1-
|
| ||
(1-
|
| ||
(1-
|
| n |
 |
| k=2 |
| n |
 |
| k=2 |
| 1 | |||||
|
| 1 | |||||
|
| 1 |
| 1+a2 |
| 1 | ||||
1+an+
|
| 4 |
| 5 |
| 1 | ||||
1+an+
|


科目:高中数学 来源: 题型:
 在xoy平面上有一系列点P1(x1,y1),P2(x2,y2)…,Pn(xn,yn),…,(n∈N*),点Pn在函数y=x2(x≥0)的图象上,以点Pn为圆心的圆Pn与x轴都相切,且圆Pn与圆Pn+1又彼此外切.若x1=1,且xn+1<xnx1=1.
在xoy平面上有一系列点P1(x1,y1),P2(x2,y2)…,Pn(xn,yn),…,(n∈N*),点Pn在函数y=x2(x≥0)的图象上,以点Pn为圆心的圆Pn与x轴都相切,且圆Pn与圆Pn+1又彼此外切.若x1=1,且xn+1<xnx1=1.| S1 |
| S2 |
| Sn |
3
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
(1)求证:数列{1xn}是等差数列;
(2)设⊙Pn的面积为Sn,Tn=![]() +…+
+…+![]() ,求证:Tn<
,求证:Tn<![]() .
.
查看答案和解析>>
科目:高中数学 来源:2008年浙江省温州市摇篮杯高一数学竞赛试卷(解析版) 题型:解答题
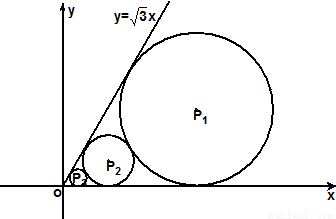
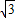 x,(x≥0)都相切,且⊙Pn与⊙Pn+1彼此外切.若x1=1,且xn+1<xn(n∈N*).
x,(x≥0)都相切,且⊙Pn与⊙Pn+1彼此外切.若x1=1,且xn+1<xn(n∈N*).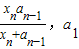 =1,
=1,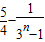 ,(n≥2)
,(n≥2)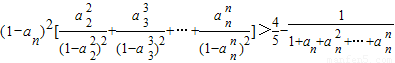 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com