
【题目】说明:请考生在(A)、(B)两个小题中任选一题作答。
(A)已知函数![]() ;
;
(1)求![]() 的零点;
的零点;
(2)若![]() 有三个零点,求实数
有三个零点,求实数![]() 的取值范围.
的取值范围.
(B)已知函数![]()
(1)求![]() 的零点;
的零点;
(2)若 ,
,![]() 有4个零点,求
有4个零点,求![]() 的取值范围.
的取值范围.
【答案】(A)(1)![]() ,
,![]() (2)
(2)![]() (B)(1)
(B)(1)![]() ,
,![]() ,
,![]() ,-1(2)
,-1(2)![]()
【解析】
(A)(1)分![]() 和
和![]() 解方程即可得到答案;(2)结合函数
解方程即可得到答案;(2)结合函数![]() 的单调性及值域,分2种情况
的单调性及值域,分2种情况![]() 与
与![]() 讨论即可。
讨论即可。
(B)(1)结合函数表达式,可得到![]() 或
或![]() ,解方程即可;(2)结合函数
,解方程即可;(2)结合函数![]() 与
与![]() 的单调性与值域,分三种情况
的单调性与值域,分三种情况![]() ,
,![]() ,
,![]() 讨论即可。
讨论即可。
(A)(1)当![]() 时,
时,![]() ,∴
,∴![]() ,∴
,∴![]() ;当
;当![]() 时,
时,![]() ,∴
,∴![]() ,∴
,∴![]() ∴
∴![]() 的零点是
的零点是![]() ,
,![]() .
.
(2)![]() 在
在![]() 上,单调递增,值域是
上,单调递增,值域是![]() ,在
,在![]() 上,单调递增,值域为
上,单调递增,值域为![]() ,如图:
,如图:
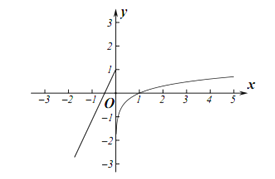
若![]() 有三个零点,
有三个零点,
令![]() ,
,![]() 时,
时,![]() 有1个解,
有1个解,![]() 时,
时,![]() 有2个解,
有2个解,
则当![]() ,
,![]() 有2个解,不成立,
有2个解,不成立,
当![]() 时,
时,![]() 有1个解,则
有1个解,则![]() ,即
,即![]() ,满足题意。
,满足题意。
(B)(1)由![]() 得
得![]() 或
或![]() ,
,
当![]() 时,
时,![]() ,或者
,或者![]() ,
,
当![]() ,
,![]() ,-1,
,-1,
故![]() 的零点为
的零点为![]() ,
,![]() ,
,![]() ,-1.
,-1.
(2)![]() 在
在![]() 上,单调递增,值域是
上,单调递增,值域是![]() ,在
,在![]() 上,单调递增,值域为
上,单调递增,值域为![]() ,
,![]() 在
在![]() 上,单调递增,值域为
上,单调递增,值域为![]() ,在
,在![]() 上,单调递增,值域为
上,单调递增,值域为![]() ,
,
令![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() 只有一个解,
只有一个解,![]() ,不成立;
,不成立;
当![]() 时,
时,![]() 有2个解
有2个解![]() ,
,![]() ,
,![]() ,
,
若![]() 时,
时,![]() 有两解,若
有两解,若![]() 时,
时,![]() 最多1个解,
最多1个解,
即![]() 时,
时,![]() 至多三个解,不合题意。
至多三个解,不合题意。
当![]() 时,
时,![]() 有2个解
有2个解![]() ,
,![]() ,
,![]() ,
,
若![]() 时,
时,![]() 有2解,若
有2解,若![]() 时,
时,![]() 有2解,
有2解,
即![]() 时,
时,![]() 有4个解,满足题意。
有4个解,满足题意。
故![]() .
.


 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案 互动课堂系列答案
互动课堂系列答案科目:高中数学 来源: 题型:
【题目】如图,△ABC是圆的内接三角形,∠BAC的平分线交圆于点D,交BC于E,过点B的圆的切线与AD的延长线交于点F,在上述条件下,给出下列四个结论:
①BD平分∠CBF;
②FB2=FDFA;
③AECE=BEDE;
④AFBD=ABBF.
所有正确结论的序号是( )
A.①②
B.③④
C.①②③
D.①②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,
,![]() .
.
(1)当![]() 时,函数
时,函数![]() ,
,![]() 在
在![]() 处的切线互相垂直,求
处的切线互相垂直,求![]() 的值;
的值;
(2)当函数![]() 在定义域内不单调时,求证:
在定义域内不单调时,求证:![]() ;
;
(3)是否存在实数![]() ,使得对任意
,使得对任意![]() ,都有函数
,都有函数![]() 的图象在
的图象在![]() 的图象的下方?若存在,请求出最大整数
的图象的下方?若存在,请求出最大整数![]() 的值;若不存在,请说理由.(参考数据:
的值;若不存在,请说理由.(参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某公司要在A、B两地连线上的定点C处建造广告牌CD,其中D为顶端,AC长35米,CB长80米,设点A、B在同一水平面上,从A和B看D的仰角分别为α和β. 
(1)设计中CD是铅垂方向,若要求α≥2β,问CD的长至多为多少(结果精确到0.01米)?
(2)施工完成后,CD与铅垂方向有偏差,现在实测得α=38.12°,β=18.45°,求CD的长(结果精确到0.01米).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某中学举行的电脑知识竞赛中,将高一年级两个班参赛的学生成绩进行整理后分成五组,绘制如图所示的频率分布直方图.已知图中从左到右的第一,第三,第四,第五小组的频率分别是0.30,0.15,0.10,0.05,第二小组的频数是40.
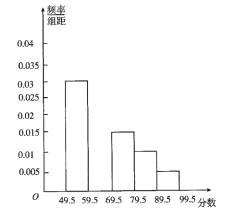
(1)补齐图中频率分布直方图,并求这两个班参赛学生的总人数;
(2)利用频率分布直方图,估算本次比赛学生成绩的平均数和中位数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个机器人每一秒钟前进一步或后退一步,程序设计师设计的程序是让机器人以先前进3步,然后再后退2步的规律移动.如果将机器人放在数轴的原点,面向正的方向在数轴上移动(1步的距离为1个单位长度).令![]() 表示第
表示第![]() 秒时机器人所在位置的坐标,且记
秒时机器人所在位置的坐标,且记![]() ,则下列结论中错误的是( )
,则下列结论中错误的是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com