
分析 (1)求出f(x)的导数,可得切线的斜率,由点斜式方程即可得到所求切线的方程;
(2)设切点(m,$\frac{4}{m}$),求得切线的斜率和方程,代入(2,0),解方程可得m,即可得到所求切线的方程.
解答 解:(1)f(x)=$\frac{4}{x}$的导数为f′(x)=-$\frac{4}{{x}^{2}}$,
可得切线的斜率为k=-1,
切线的方程为y-2=-(x-2),
即为x+y-4=0;
(2)设切点(m,$\frac{4}{m}$),
可得切线的方程为y-$\frac{4}{m}$=-$\frac{4}{{m}^{2}}$(x-m),
即为y=-$\frac{4}{{m}^{2}}$x+$\frac{8}{m}$,
代入(2,0),可得0=-$\frac{4}{{m}^{2}}$•2+$\frac{8}{m}$,
解得m=1(0舍去),
可得过B(2,0)的直线方程为y-0=-4(x-2),
即有4x+y-8=0.
点评 本题考查导数的运用:求切线方程,考查导数的几何意义,注意区分在某点处和过某点的切线,考查方程思想,运算化简能力,属于中档题.


 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案科目:高中数学 来源: 题型:解答题
| 停靠时间 | 2.5 | 3 | 3.5 | 4 | 4.5 | 5 | 5.5 | 6 |
| 轮船数量 | 12 | 12 | 17 | 20 | 15 | 13 | 8 | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -11 | B. | 46 | C. | 77 | D. | -76 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
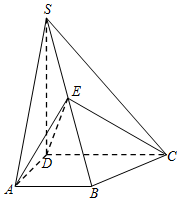 如图,在四棱锥S-ABCD中,已知SD⊥底面ABCD,且四边形ABCD为直角梯形,∠DAB=∠ADC=$\frac{π}{2}$,SD=DC=2,AD=AB=1,E为棱SB上的一点,且DE⊥SC.
如图,在四棱锥S-ABCD中,已知SD⊥底面ABCD,且四边形ABCD为直角梯形,∠DAB=∠ADC=$\frac{π}{2}$,SD=DC=2,AD=AB=1,E为棱SB上的一点,且DE⊥SC.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com