
| A. | f($\frac{1}{3}$)<f(2)<f($\frac{1}{2}$) | B. | f($\frac{1}{2}$)<f(2)<f($\frac{1}{3}$) | C. | f($\frac{1}{2}$)<f($\frac{1}{3}$)<f(2) | D. | f(2)<f($\frac{1}{3}$)<f($\frac{1}{2}$) |
分析 由已知得函数f(x)的图象关于直线x=1对称,⇒函数f(x)在(1,+∞)上递增,在(-∞,1)上递减,⇒f($\frac{1}{2}$)<f($\frac{1}{3}$)<f(0),及f($\frac{1}{2}$)<f($\frac{1}{3}$)<f(2).
解答 解:函数f(x)定义在实数集R上,且满足f(1+x)=f(1-x),
∴函数f(x)的图象关于直线x=1对称,∴f(2)=f(0).
又∵当x≥1时,f(x)=2x,∴函数f(x)在(1,+∞)上递增,在(-∞,1)上递减,
∴f($\frac{1}{2}$)<f($\frac{1}{3}$)<f(0),及f($\frac{1}{2}$)<f($\frac{1}{3}$)<f(2).
故选:C.
点评 本题考查了函数的对称性及单调性,属于中档题.


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | {an}的各项均为正数 | B. | {an}的各项均为负数 | ||
| C. | {an}为递增数列 | D. | {an}为递减数列 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
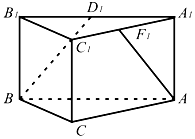 如图,直三棱柱ABC-A1B1C1中,∠BCA=90°,点D1,F1分别是A1B1,A1C1的中点,若BC=CA=2CC1,则BD1与AF1所成的角是( )
如图,直三棱柱ABC-A1B1C1中,∠BCA=90°,点D1,F1分别是A1B1,A1C1的中点,若BC=CA=2CC1,则BD1与AF1所成的角是( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{16}$=1 | B. | $\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{9}$=1 | C. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{9}$=1 | D. | $\frac{5{x}^{2}}{16}$-$\frac{5{y}^{2}}{9}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 垂直于同一条直线的两条直线相互垂直 | |
| B. | 若一条直线平行于两个相交平面,则这条直线与这两个平面的交线平行 | |
| C. | 若一个平面经过另一个平面的垂线,那么这两个平面相互垂直 | |
| D. | 若一个平面内的两条相交直线与另一个平面内的相交直线分别平行,那么这两个平面相互平行 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图正三棱柱ABC-A1B1C1中,底面边长为a,侧棱长为$\frac{{\sqrt{2}}}{2}a$,若经过对角线AB1且与对角线BC1平行的平面交上底面于DB1.
如图正三棱柱ABC-A1B1C1中,底面边长为a,侧棱长为$\frac{{\sqrt{2}}}{2}a$,若经过对角线AB1且与对角线BC1平行的平面交上底面于DB1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com