
【题目】已知f(x)=a(x-lnx)+![]() ,a∈R.
,a∈R.
(I)讨论f(x)的单调性;
(II)当a=1时,证明f(x)>f’(x)+![]() 对于任意的x∈[1,2] 恒成立。
对于任意的x∈[1,2] 恒成立。
【答案】(I)见解析;(II)见解析.
【解析】试题分析:(Ⅰ)求出原函数的导函数,然后对a分类分析导函数的符号,由导函数的符号确定原函数的单调性;
(Ⅱ)令g(x)=x-lnx,h(x)=![]() -1则f(x)-f′(x)=g(x)+h(x),利用导数分别求g(x)与h(x)的最小值得到f(x)-f’(x)>g(1)+h(2)=
-1则f(x)-f′(x)=g(x)+h(x),利用导数分别求g(x)与h(x)的最小值得到f(x)-f’(x)>g(1)+h(2)=![]() .
.
试题解析:
(I)解:函数的定义域为(0,+00),f’(x)=a-![]()
F’(x)=![]()
若a≤0时,x∈(0,1)时,f’(x)>0,则f(x)单调递增
x∈(1,+00)时,f’(x)<0,则f(x)单调递减。
当a>0时,f’(x)=![]() (
(![]() )(x-
)(x-![]() )
)
若0<a<2时,![]() >1,
>1,
当x∈(0,1)或x∈(![]() ,+00)时,f’(x)>0,f(x)单调递增
,+00)时,f’(x)>0,f(x)单调递增
当x∈(1,![]() )时,f’(x)<0,f(x)单调递减。
)时,f’(x)<0,f(x)单调递减。
若a=2时,![]() =1,早x∈(0,+00)内,f’(x)≥0,f(x)单调递增;
=1,早x∈(0,+00)内,f’(x)≥0,f(x)单调递增;
若a>2时,0<![]() <1,
<1,
当x∈(0,![]() )或x∈(1,+00)时,f’(x)>0,f(x)单调递增
)或x∈(1,+00)时,f’(x)>0,f(x)单调递增
当x∈(![]() ,1)时,f‘(x)<0,f(x)单调递减。
,1)时,f‘(x)<0,f(x)单调递减。
综上所述;当a≤0时,f(x)在(0,1)单调递增,f(x)在(1,+00)单调递减。
当0<a<2时,f(x)在(0,1)上单调递增;f(x)在(1,![]() )单调递减
)单调递减
当a=2时,f(x)在(0,+00)单调递增;
若a>2时,f(x)在(0,![]() ),(1,+00)单调递增;
),(1,+00)单调递增;
f(x)在(![]() ,1)单调递减
,1)单调递减
(II)由(I)知,a=1时,f(x)-f’(x)=x-lnx+![]() -(1-
-(1-![]() )
)
=x-lnx+![]() -1,x∈[1,2]
-1,x∈[1,2]
令g(x)=x-lnx,h(x)=![]() -1,x∈[1,2],则f(x)-f’(x)=g(x)+h(x),
-1,x∈[1,2],则f(x)-f’(x)=g(x)+h(x),
由g’(x)=![]() ≥0,可得g(x)≥g(1)=1,当且仅当x=1时取得等号,
≥0,可得g(x)≥g(1)=1,当且仅当x=1时取得等号,
又h’(x)=![]() ,设
,设![]() (x)=-3x2-2x+6,则
(x)=-3x2-2x+6,则![]() (x)在x∈[1,2]单调递减,
(x)在x∈[1,2]单调递减,
因为![]() (1)=1,
(1)=1,![]() (2)=-10,所以在[1,2]上存在x0,
(2)=-10,所以在[1,2]上存在x0,
使得x∈(1,x0)时,![]() (x)>0,x∈(x0,2)时,
(x)>0,x∈(x0,2)时,![]() (x)<0.
(x)<0.
所以h(x)在(1,x0)上单调递增,在(x0,2)上单调递减;
由于h(1)=1,h(2)=![]() ,因此h(x)≥h(2)=
,因此h(x)≥h(2)=![]() ,当且仅当x=2时取得等号
,当且仅当x=2时取得等号
所以f(x)-f’(x)>g(1)+h(2)=![]() ,
,
即f(x)>f’(x)+![]() 对于任意的x∈[1,2]恒成立。
对于任意的x∈[1,2]恒成立。


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知在四棱锥P﹣ABCD中,底面ABCD是矩形,且AD=2,AB=1,PA⊥平面ABCD,E、F分别是线段AB、BC的中点. 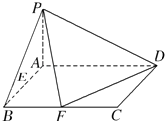
(Ⅰ)证明:PF⊥FD;
(Ⅱ)判断并说明PA上是否存在点G,使得EG∥平面PFD;
(Ⅲ)若PB与平面ABCD所成的角为45°,求二面角A﹣PD﹣F的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)对任意实数x,y恒有f(x+y)=f(x)+f(y),且当x>0时,f(x)<0,又f(1)=﹣2.
(1)判断f(x)的奇偶性及单调性并证明你的结论;
(2)若对任意x∈R,不等式f(ax2)﹣2f(x)<f(x)+4恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ,数列{an}满足a1=1,an+1=f(
,数列{an}满足a1=1,an+1=f( ![]() ),n∈N* .
),n∈N* .
(1)求数列{an}的通项公式;
(2)令bn= ![]() (n≥2),b1=3,Sn=b1+b2++bn , 若Sn<
(n≥2),b1=3,Sn=b1+b2++bn , 若Sn< ![]() 对一切n∈N*成立,求最小正整数m.
对一切n∈N*成立,求最小正整数m.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋子里有完全相同的3只红球和4只黑球,今从袋子里随机取球.
(Ⅰ)若有放回地取3次,每次取一个球,求取出2个红球1个黑球的概率;
(Ⅱ)若无放回地取3次,每次取一个球,若取出每只红球得2分,取出每只黑球得1分,求得分![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,曲线![]() 的参数方程为
的参数方程为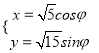 (
(![]() 为参数),直线
为参数),直线![]() 的参数方程为
的参数方程为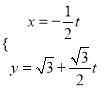 (
(![]() 为参数).以原点为极点,
为参数).以原点为极点, ![]() 轴的正半轴为极轴建立极坐标系,点
轴的正半轴为极轴建立极坐标系,点![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求点![]() 的直角坐标,并求曲线
的直角坐标,并求曲线![]() 的普通方程;
的普通方程;
(2)设直线![]() 与曲线
与曲线![]() 的两个交点为
的两个交点为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的偶函数f(x),满足f(x+1)=f(x﹣1),且f(x)在[﹣3,﹣2]上是增函数,又α、β是锐角三角形的两个内角,则( )
A.f(sinα)>f(cosβ)
B.f(cosα)<f(cosβ)
C.f(sinα)<f(cosβ)
D.f(sinα)<f(sinβ)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com