
【题目】如图,在下列三个正方体![]() 中,
中,![]() 均为所在棱的中点,过
均为所在棱的中点,过![]() 作正方体的截面.在各正方体中,直线
作正方体的截面.在各正方体中,直线![]() 与平面
与平面![]() 的位置关系描述正确的是
的位置关系描述正确的是
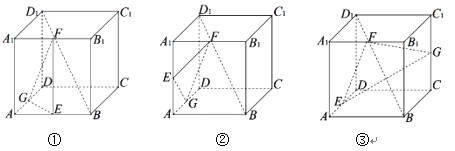
A. ![]() 平面
平面![]() 的有且只有①;
的有且只有①;![]() 平面
平面![]() 的有且只有②③
的有且只有②③
B. ![]() 平面
平面![]() 的有且只有②;
的有且只有②;![]() 平面
平面![]() 的有且只有①
的有且只有①
C. .![]() 平面
平面![]() 的有且只有①;
的有且只有①;![]() 平面
平面![]() 的有且只有②
的有且只有②
D. ![]() 平面
平面![]() 的有且只有②;
的有且只有②;![]() 平面
平面![]() 的有且只有③
的有且只有③
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案科目:高中数学 来源: 题型:
【题目】某高校为增加应届毕业生就业机会,每年根据应届毕业生的综合素质和学业成绩对学生进行综合评估,已知某年度参与评估的毕业生共有2000名.其评估成绩![]() 近似的服从正态分布
近似的服从正态分布![]() .现随机抽取了100名毕业生的评估成绩作为样本,并把样本数据进行了分组,绘制了如下频率分布直方图:
.现随机抽取了100名毕业生的评估成绩作为样本,并把样本数据进行了分组,绘制了如下频率分布直方图:
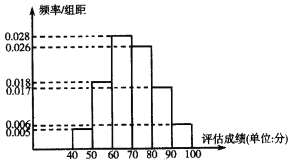
(1)求样本平均数![]() 和样本方差
和样本方差![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(2)若学校规定评估成绩超过82.7分的毕业生可参加![]() 三家公司的面试.
三家公司的面试.
用样本平均数![]() 作为的估计值
作为的估计值![]() ,用样本标准差
,用样本标准差![]() 作为
作为![]() 的估计值
的估计值![]() .请利用估计值判断这2000名毕业生中,能够参加三家公司面试的人数;
.请利用估计值判断这2000名毕业生中,能够参加三家公司面试的人数;
附:![]() 若随机变量
若随机变量![]() ,则
,则![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了节能减排,发展低碳经济,我国政府从2001年起就通过相关扶植政策推动新能源汽车产业发展.下面的图表反映了该产业发展的相关信息:
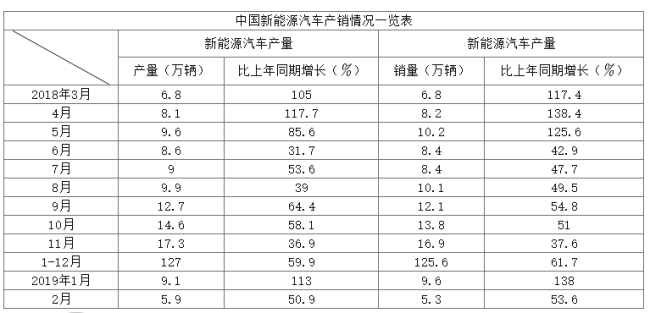
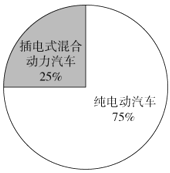
2019年2月份新能源汽车销量结构图根据上述图表信息,下列结论错误的是( )
A.2018年4月份我国新能源汽车的销量高于产量
B.2017年3月份我国新能源汽车的产量不超过3.4万辆
C.2019年2月份我国插电式混合动力汽车的销量低于1万辆
D.2017年我国新能源汽车总销量超过70万辆
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为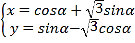 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴,取相同长度单位建立极坐标系,直线
轴的正半轴为极轴,取相同长度单位建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求曲线![]() 和直线
和直线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)直线![]() 与
与![]() 轴交点为
轴交点为![]() ,经过点
,经过点![]() 的直线与曲线
的直线与曲线![]() 交于
交于![]() ,
,![]() 两点,证明:
两点,证明:![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 、
、![]() 、
、![]() ,对于给定的正整数
,对于给定的正整数![]() ,记
,记![]() ,
,![]()
![]() .若对任意的正整数
.若对任意的正整数![]() 满足:
满足:![]() ,且
,且![]() 是等差数列,则称数列
是等差数列,则称数列![]() 为“
为“![]() ”数列.
”数列.
(1)若数列![]() 的前
的前![]() 项和为
项和为![]() ,证明:
,证明:![]() 为
为![]() 数列;
数列;
(2)若数列![]() 为
为![]() 数列,且
数列,且![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(3)若数列![]() 为
为![]() 数列,证明:
数列,证明:![]() 是等差数列 .
是等差数列 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为响应党中央“扶贫攻坚”的号召,某单位指导一贫困村通过种植紫甘薯来提高经济收入.紫甘薯对环境温度要求较高,根据以往的经验,随着温度的升高,其死亡株数成增长的趋势.下表给出了2017年种植的一批试验紫甘薯在温度升高时6组死亡的株数:

经计算: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,其中
,其中![]() 分别为试验数据中的温度和死亡株数,
分别为试验数据中的温度和死亡株数, ![]() .
.
(1)若用线性回归模型,求![]() 关于
关于![]() 的回归方程
的回归方程![]() (结果精确到
(结果精确到![]() );
);
(2)若用非线性回归模型求得![]() 关于
关于![]() 的回归方程为
的回归方程为![]() ,且相关指数为
,且相关指数为![]() .
.
(i)试与(1)中的回归模型相比,用![]() 说明哪种模型的拟合效果更好;
说明哪种模型的拟合效果更好;
(ii)用拟合效果好的模型预测温度为![]() 时该批紫甘薯死亡株数(结果取整数).
时该批紫甘薯死亡株数(结果取整数).
附:对于一组数据![]() ,
, ![]() ,……,
,……, ![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: 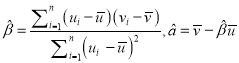 ;相关指数为:
;相关指数为: 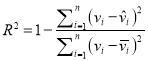 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给定椭圆![]() :
:![]() ,称圆心在原点
,称圆心在原点![]() ,半径为
,半径为![]() 的圆是椭圆
的圆是椭圆![]() 的“伴椭圆”,若椭圆
的“伴椭圆”,若椭圆![]() 的一个焦点为
的一个焦点为![]() ,其短轴上一个端点到
,其短轴上一个端点到![]() 的距离为
的距离为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 作椭圆
作椭圆![]() 的“伴随圆”
的“伴随圆”![]() 的动弦
的动弦![]() ,过点
,过点![]() 、
、![]() 分别作“伴随圆”
分别作“伴随圆”![]() 的切线,设两切线交于点
的切线,设两切线交于点![]() ,证明:点
,证明:点![]() 的轨迹是直线,并写出该直线的方程;
的轨迹是直线,并写出该直线的方程;
(3)设点![]() 是椭圆
是椭圆![]() 的“伴随圆”
的“伴随圆”![]() 上的一个动点,过点
上的一个动点,过点![]() 作椭圆
作椭圆![]() 的切线
的切线![]() 、
、![]() ,试判断直线
,试判断直线![]() 、
、![]() 是否垂直?并说明理由.
是否垂直?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com