
【题目】已知数列![]() 中
中
![]() .
.
(1)是否存在实数![]() ,使数列
,使数列![]() 是等比数列?若存在,求
是等比数列?若存在,求![]() 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
(2)若![]() 是数列
是数列![]() 的前
的前![]() 项和,求满足
项和,求满足![]() 的所有正整数
的所有正整数![]() .
.
【答案】(1)![]() (2)1和2.
(2)1和2.
【解析】
试题分析:(1)判断数列是否为等比数列,一般利用定义:即判断
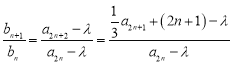
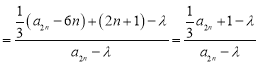 是否为常数,这时有两个思路,一是从特殊出发,先探索常数,再证明其对于任意皆成立;二是从一般出发,利用恒等式的条件求出常数,(2)(1)提供了求和的方法:先求出
是否为常数,这时有两个思路,一是从特殊出发,先探索常数,再证明其对于任意皆成立;二是从一般出发,利用恒等式的条件求出常数,(2)(1)提供了求和的方法:先求出![]() ,再由
,再由![]() ,得
,得![]() ,
,![]()
![]() ,因此
,因此![]() ,以下结合单调性解不等式
,以下结合单调性解不等式![]() 即可.
即可.
试题解析:解:(1)设![]() ,
,
因为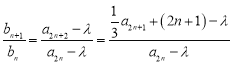
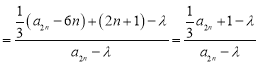 . 2分
. 2分
若数列![]() 是等比数列,则必须有
是等比数列,则必须有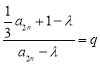 (常数),
(常数),
即![]() ,即
,即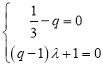
![]()
![]() , 5分
, 5分
此时![]() ,
,
所以存在实数![]() ,使数列
,使数列![]() 是等比数列 6分
是等比数列 6分
(注:利用前几项,求出![]() 的值,并证明不扣分)
的值,并证明不扣分)
(2)由(1)得![]() 是以
是以![]() 为首项,
为首项,![]() 为公比的等比数列,
为公比的等比数列,
故![]() ,即
,即![]() , 8分
, 8分
由![]() ,得
,得![]() , 10分
, 10分
所以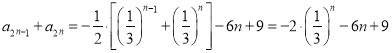 ,
,
![]()
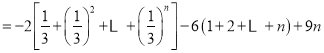

![]() , 12分
, 12分
显然当![]() 时,
时,![]() 单调递减,
单调递减,
又当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,所以当
,所以当![]() 时,
时,![]() ;
;
![]() ,
,
同理,当且仅当![]() 时,
时,![]() .
.
综上,满足![]() 的所有正整数
的所有正整数![]() 为1和2. 16分
为1和2. 16分


 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案科目:高中数学 来源: 题型:
【题目】一个几何体的三视图如图所示,其中正视图和侧视图是腰长为2的两个全等的等腰直角三角形,则该几何体的外接球的表面积是( ) 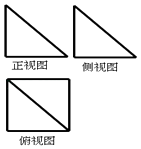
A.![]()
B.4 ![]() π
π
C.12π
D.![]() π
π
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知中心在坐标原点,焦点在x轴上的椭圆,离心率为 ![]() 且过点(
且过点( ![]() ,0),过定点C(﹣1,0)的动直线与该椭圆相交于A、B两点.
,0),过定点C(﹣1,0)的动直线与该椭圆相交于A、B两点.
(1)若线段AB中点的横坐标是﹣ ![]() ,求直线AB的方程;
,求直线AB的方程;
(2)在x轴上是否存在点M,使 ![]() 为常数?若存在,求出点M的坐标;若不存在,请说明理由.
为常数?若存在,求出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分14分)某学校为了支持生物课程基地研究植物生长,计划利用学校空地建造一间室内面积为900m2的矩形温室,在温室内划出三块全等的矩形区域,分别种植三种植物,相邻矩形区域之间间隔1m,三块矩形区域的前、后与内墙各保留 1m 宽的通道,左、右两块矩形区域分别与相邻的左右内墙保留 3m 宽的通道,如图.设矩形温室的室内长为![]() (m),三块种植植物的矩形区域的总面积为
(m),三块种植植物的矩形区域的总面积为![]() (m2).
(m2).
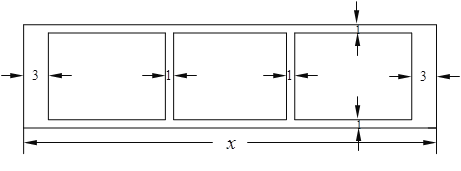
(1)求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于三角形满足的条件,下列判断正确的是( )
A.a=7,b=14,A=30°,有两解
B.a=30,b=25,A=150°,有一解
C.a=6,b=9,A=45°,有两解
D.b=9,c=10,B=60°,无解
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本题满分14分)如图,我市有一个健身公园,由一个直径为2km的半圆和一个以![]() 为斜边的等腰直角三角形
为斜边的等腰直角三角形![]() 构成,其中
构成,其中![]() 为
为![]() 的中点.现准备在公园里建设一条四边形健康跑道
的中点.现准备在公园里建设一条四边形健康跑道![]() ,按实际需要,四边形
,按实际需要,四边形![]() 的两个顶点
的两个顶点![]() 分别在线段
分别在线段![]() 上,另外两个顶点
上,另外两个顶点![]() 在半圆上,
在半圆上, ![]() ,且
,且![]() 间的距离为1km.设四边形
间的距离为1km.设四边形![]() 的周长为
的周长为![]() km.
km.

(1)若![]() 分别为
分别为![]() 的中点,求
的中点,求![]() 长;
长;
(2)求周长![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=x2+2ax﹣b2+4
(1)若a是从0,1,2三个数中任取的一个数,b是从﹣2,﹣1,0,1,2五个数中任取的一个数,求函数f(x)有零点的概率;
(2)若a是从区间[﹣3,3]上任取的一个数,b是从区间[0,3]上任取的一个数,求函数g(x)=f(x)+5无零点的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,长方体ABCD﹣A1B1C1D1中,AB=16,BC=10,AA1=8,点E,F分别在A1B1 , D1C1上,A1E=D1F=4,过点E,F的平面α与此长方体的面相交,交线围成一个正方形. 
(I)在图中画出这个正方形(不必说明画法和理由);
(II)求直线AF与平面α所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{![]() }中,
}中, ![]() ,且
,且![]() 对任意正整数都成立,数列{
对任意正整数都成立,数列{![]() }的前n项和为Sn。
}的前n项和为Sn。
(1)若![]() ,且
,且![]() ,求a;
,求a;
(2)是否存在实数k,使数列{![]() }是公比不为1的等比数列,且任意相邻三项
}是公比不为1的等比数列,且任意相邻三项![]() 按某顺序排列后成等差数列,若存在,求出所有k值,若不存在,请说明理由;
按某顺序排列后成等差数列,若存在,求出所有k值,若不存在,请说明理由;
(3)若![]() 。
。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com