
| AΘ° | $\frac{Π–}{6}$ | BΘ° | $\frac{Π–}{3}$ | CΘ° | $\frac{2Π–}{3}$ | DΘ° | $\frac{5Π–}{6}$ |
Ζ÷Έω ΗυΨί–¬Ε®“ε«σΒΟfΘ®xΘ©ΒΡΫβΈω ΫΘ§‘Όάϊ”ΟΚ· ΐy=AsinΘ®ΠΊx+Π’Θ©ΒΡΆΦœσ±δΜΜΙφ¬…Θ§’ΐœ“Κ· ΐΒΡΆΦœσΒΡΕ‘≥Τ–‘Θ§«σΒΟΠ’ΒΡΉν–Γ÷ΒΘ°
Ϋβ¥π ΫβΘΚΫΪΚ· ΐfΘ®xΘ©=$|\begin{array}{l}{sinx}&{cosx}\\{1}&{\sqrt{3}}\end{array}|$=$\sqrt{3}$sinx-cosx=2sinΘ®x-$\frac{Π–}{6}$Θ©ΒΡΆΦœσœρ”“ΤΫ“ΤΠ’Θ®Π’ΘΨ0Θ©ΗωΒΞΈΜΚσΘ§
Ω…ΒΟy=2sinΘ®x-Π’-$\frac{Π–}{6}$Θ©ΒΡΆΦœσΘ°
ΗυΨίΥυΒΟΆΦœσΕ‘”ΠΒΡΚ· ΐΈΣΤφΚ· ΐΘ§Ω…ΒΟΠ’+$\frac{Π–}{6}$=kΠ–Θ§kΓ ZΘ§Φ¥Π’=kΠ–-$\frac{Π–}{6}$Θ§kΓ ZΘ§
Υυ“‘Π’ΒΡΉν–Γ÷Β «$\frac{5Π–}{6}$Θ§
Ι ―ΓΘΚDΘ°
ΒψΤά ±ΨΧβ÷ς“ΣΩΦ≤ι–¬Ε®“εΘ§Κ· ΐy=AsinΘ®ΠΊx+Π’Θ©ΒΡΆΦœσ±δΜΜΙφ¬…Θ§’ΐœ“Κ· ΐΒΡΆΦœσΒΡΕ‘≥Τ–‘Θ§ τ”ΎΜυ¥ΓΧβΘ°



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° | -$\frac{\sqrt{3}}{2}$ | BΘ° | -$\frac{1}{2}$ | CΘ° | $\frac{1}{2}$ | DΘ° | $\frac{\sqrt{3}}{2}$ |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° | 0 | BΘ° | 1 | CΘ° | 2 | DΘ° | 3 |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΧνΩ’Χβ
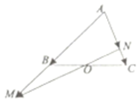 »γΆΦΥυ ΨΘ§‘ΎΓςABC÷–Θ§ΒψO «BCΒΡ÷–ΒψΘ§ΙΐΒψOΒΡ÷±œΏΖ÷±πΫΜ÷±œΏABΘ§AC”Ύ≤ΜΆ§ΒΡΝΫΒψMΘ§NΘ§»τ$\overrightarrow{AB}$=$\frac{3}{5}$$\overrightarrow{AM}$Θ§$\overrightarrow{AC}$=m$\overrightarrow{AN}$Θ§‘ρmΒΡ÷ΒΈΣ$\frac{7}{5}$Θ°
»γΆΦΥυ ΨΘ§‘ΎΓςABC÷–Θ§ΒψO «BCΒΡ÷–ΒψΘ§ΙΐΒψOΒΡ÷±œΏΖ÷±πΫΜ÷±œΏABΘ§AC”Ύ≤ΜΆ§ΒΡΝΫΒψMΘ§NΘ§»τ$\overrightarrow{AB}$=$\frac{3}{5}$$\overrightarrow{AM}$Θ§$\overrightarrow{AC}$=m$\overrightarrow{AN}$Θ§‘ρmΒΡ÷ΒΈΣ$\frac{7}{5}$Θ°≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° | fΘ®xΘ©=x2-4x | BΘ° | gΘ®xΘ©=3x+1 | CΘ° | hΘ®xΘ©=3-x | DΘ° | tΘ®xΘ©=tanx |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΑΌΕ»÷¬–≈ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com