
分析 (1)首先由题意画出示意图,求出图上距离AB;
(2)然后解三角形AOC,利用余弦定理求出OC长度,在三角形COD中求∠COD的正切即可.
解答 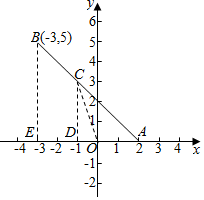 解:(1)由题意如图,|AB|=$\sqrt{(2+3)^{2}+{5}^{2}}=5\sqrt{2}$,
解:(1)由题意如图,|AB|=$\sqrt{(2+3)^{2}+{5}^{2}}=5\sqrt{2}$,
所以此人行走了500$\sqrt{2}$m,在出发点的西偏北45°方向,速度是50$\sqrt{2}$m/min;
(2)由(1)可得AC的实际距离为300$\sqrt{2}$m,图上距离为3$\sqrt{2}$,
在三角形OAC中,OC2=OA2+AC2-2OA•AC•cos45°=4+18-2×2×3$\sqrt{2}$×$\frac{\sqrt{2}}{2}$=10,所以OC=$\sqrt{10}$;
由AC:AB=CD:BE=3:5,得到CD=3,所以tan∠AOC=-$\frac{CD}{OD}$=-3,所以∠COD=90°-18°26'=71°34';
所以少年宫C点相对于广场中心西偏北71°34',距离O为100$\sqrt{10}$m.
点评 本题考查了解三角形在实际中的应用;正确画出示意图,利用余弦定理解三角形,求出OC长度是关键.


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:高中数学 来源: 题型:选择题
| A. | a<b<c | B. | a<c<b | C. | b<c<a | D. | c<a<b |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{4}$-$\frac{1}{3}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{2}$ | D. | $\frac{π}{2}$+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com