
【题目】PM2.5是衡量空气质量的重要指标,我国采用世卫组织的最宽值限定值,即PM2.5日均值在![]() 以下空气质量为一级,在
以下空气质量为一级,在![]() 空气质量为二级,超过
空气质量为二级,超过![]() 为超标,如图是某地1月1日至10日的PM2.5(单位:
为超标,如图是某地1月1日至10日的PM2.5(单位:![]() )的日均值,则下列说法正确的是( )
)的日均值,则下列说法正确的是( )
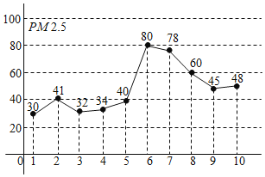
A.10天中PM2.5日均值最低的是1月3日
B.从1日到6日PM2.5日均值逐渐升高
C.这10天中恰有5天空气质量不超标
D.这10天中PM2.5日均值的中位数是43
科目:高中数学 来源: 题型:
【题目】现在进入“互联网+”时代,大学生小张自己开了一家玩具店,他通过“互联网+”销售某种玩具,经过一段时间对一种玩具的销售情况进行统计,得5数据如下:
假定玩具的销售量![]() (百个)与玩具的销售价价格
(百个)与玩具的销售价价格![]() (元)之间存在相关关系:
(元)之间存在相关关系:
销售量 | 2 | 3 | 4 | 5 | 6 | 8 |
单个玩具的销售价 | 5.5 | 4.3 | 3.9 | 3.8 | 3.7 | 3.6 |
根据以上数据,小张分别借助甲、乙两种不同的回归模型,得到两个回归方程,方程甲:![]() ,方程乙:
,方程乙:![]() .
.
(1)以![]() 为解释变量,
为解释变量,![]() 为预报变量,作出散点图;
为预报变量,作出散点图;
(2)分别计算模型甲与模型乙的残差平方和![]() 及
及![]() ,并通过比较
,并通过比较![]() ,
,![]() 大小,判断哪个模型拟后效果更好.
大小,判断哪个模型拟后效果更好.
(3)若—个玩具进价0.5元,依据(2)中拟合效果好的模型判断该玩具店有无亏损的可能?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】三峡大坝专用公路沿途山色秀美,风景怡人.为确保安全,全程限速为80公里/小时.为了解汽车实际通行情况,经过监测发现某时段200辆汽车通过这段公路的车速均在[50,90](公里/小时)内,根据监测结果得到如下组距为10的频率分布折线图:
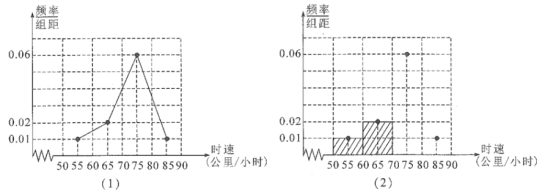
(1)请根据频率分布折线图,将颊率分布直方图补充完整(用阴影部分表示);
(2)求这200辆汽车在该路段超速的车辆数以及在该路段的平均速度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,若
,若![]() 的图象上相邻两条对称轴的距离为
的图象上相邻两条对称轴的距离为![]() ,图象过点
,图象过点![]() .
.
(1)求![]() 的表达式和
的表达式和![]() 的递增区间;
的递增区间;
(2)将函数![]() 的图象向右平移
的图象向右平移![]() 个单位长度,再将图象上各点的横坐标伸长到原来的2倍(纵坐标不变),得到函数
个单位长度,再将图象上各点的横坐标伸长到原来的2倍(纵坐标不变),得到函数![]() 的图象.若函数
的图象.若函数![]() 在区间
在区间![]() 上有且只有一个零点,求实数
上有且只有一个零点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地计划在水库建一座至多安装3台发电机的水电站.过去50年的水文资料显示,水库年入流量![]() (年入流量:一年内上游来水与库区降水之和.单位:亿立方米)都在40以上,其中,不足80的年份有10年,不低于80且不超过120的年份有35年,超过120的年份有5年,将年入流量在以上三段的频率作为相应段的概率,并假设各年的年入流量相互独立.
(年入流量:一年内上游来水与库区降水之和.单位:亿立方米)都在40以上,其中,不足80的年份有10年,不低于80且不超过120的年份有35年,超过120的年份有5年,将年入流量在以上三段的频率作为相应段的概率,并假设各年的年入流量相互独立.
(1)求未来4年中,至多有1年的年入流量超过120的概率;
(2)水电站希望安装的发电机尽可能运行,但每年发电机最多可运行台数受年入流量![]() 限制,并有如下关系:
限制,并有如下关系:
年入流量 |
|
|
|
发电机最多可运行台数 | 1 | 2 | 3 |
若某台发电机运行,则该台发电机年净利润为5000万元;若某台发电机未运行,则该台发电机年维护费与年入流量![]() 有如下关系:
有如下关系:
年入流量 |
|
|
一台未运行发电机年维护费 | 500 | 800 |
欲使水电站年净利润最大,应安装发电机多少台?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年新课标Ⅱ卷理综物理高考试题的选择题是这样的:二、选择题:本题共8小题,每小题6分,共48分,在每小题给出的四个选项中,第14~18题只有一项符合题目要求.第19~21题有多项符合题目要求,全部选对的得6分,选对但不全的得3分,有选错的得0分,每年高考后都会对每题的得分情况进行一个大致的统计,特地对第19题的得分情况进调研,从某省所有试卷中随机抽取1000份试卷,其中第19题的得分组成容量为1000的样本.统计结果如下表:
得分 | 0 | 3 | 6 |
人数 | 200 | 300 | 500 |
(1)求这1000份试卷中第19题的得分的中位数和平均数;
(2)若某校的两名高三学生因故未参加考试,如果这两名学生参加考试,以样本中各种得分情况的频率作为这两名同学相应的各种得分情况的概率.试求这两名同学理综卷第19题的得分之和![]() 的分布列及效学期望.
的分布列及效学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com