
【题目】已知函数![]() .
.
(1)若![]() 在
在![]() 上单调递减,求
上单调递减,求![]() 的取值范围;
的取值范围;
(2)若![]() 在
在![]() 处取得极值,判断当
处取得极值,判断当![]() 时,存在几条切线与直线
时,存在几条切线与直线![]() 平行,请说明理由;
平行,请说明理由;
(3)若![]() 有两个极值点
有两个极值点![]() ,求证:
,求证:![]() .
.
【答案】(Ⅰ)![]() ;(Ⅱ)答案见解析;(Ⅲ)证明见解析.
;(Ⅱ)答案见解析;(Ⅲ)证明见解析.
【解析】
(Ⅰ)由题意可得![]() 恒成立 ,构造函数,令
恒成立 ,构造函数,令![]() ,由导函数的解析式可知
,由导函数的解析式可知![]() 在
在![]() 递增,在
递增,在![]() 递减, 据此计算可得实数a的取值范围.
递减, 据此计算可得实数a的取值范围.
(Ⅱ) 由![]() 在
在![]() 处取得极值可得
处取得极值可得![]() .原问题等价于求解
.原问题等价于求解![]() 在区间
在区间![]() 内解的个数,结合导函数的解析式研究函数的单调性和函数在特殊点处的函数值即可确定切线的条数.而事实情况下检验
内解的个数,结合导函数的解析式研究函数的单调性和函数在特殊点处的函数值即可确定切线的条数.而事实情况下检验![]() 时函数
时函数![]() 不存在极值点,所以不存在满足题意的实数
不存在极值点,所以不存在满足题意的实数![]() ,也不存在满足题意的切线.
,也不存在满足题意的切线.
(Ⅲ)若函数有两个极值点![]() ,不妨设
,不妨设![]() ,易知
,易知![]() ,结合函数的解析式和零点的性质即可证得题中的不等式.
,结合函数的解析式和零点的性质即可证得题中的不等式.
(Ⅰ)由已知,![]() 恒成立
恒成立
令![]() ,
,
则![]() ,
,
![]() ,令
,令![]() ,解得:
,解得:![]() ,令
,令![]() ,解得:
,解得:![]() ,
,
故![]() 在
在![]() 递增,在
递增,在![]() 递减,
递减,
![]() ,由
,由![]() 恒成立可得
恒成立可得![]() .
.
即当![]() 在
在![]() 上单调递减时,
上单调递减时,![]() 的取值范围是
的取值范围是![]() .
.
(Ⅱ)![]() 在
在![]() 处取得极值,则
处取得极值,则![]() ,可得
,可得![]() .
.
令![]() ,即
,即 ![]() .
.
设![]() ,则
,则![]() .
.
故![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
注意到![]() ,
,![]() ,
,
则方程![]() 在
在![]() 内只有一个实数根,
内只有一个实数根,
即当![]() 时,只有一条斜率为
时,只有一条斜率为![]() 且与函数
且与函数![]() 图像相切的直线.
图像相切的直线.
但事实上,若![]() ,则
,则![]() ,
,
![]() ,
,
故函数![]() 在区间
在区间![]() 上单调递增,在区间
上单调递增,在区间![]() 上单调递减,
上单调递减,
且![]() ,故函数
,故函数![]() 在区间
在区间![]() 上恒成立,
上恒成立,
函数![]() 在区间
在区间![]() 上单调递减,即函数不存在极值点,
上单调递减,即函数不存在极值点,
即不存在满足题意的实数![]() ,也不存在满足题意的切线.
,也不存在满足题意的切线.
(Ⅲ)若函数有两个极值点![]() ,不妨设
,不妨设![]() ,
,
由(Ⅰ)可知![]() ,且:
,且:
![]() ①,
①,
![]() ②,
②,
由①-②得:![]() ,
,
即![]() ,
,
由①+②得:![]() ,
,
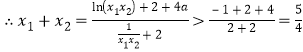 .
.


科目:高中数学 来源: 题型:
【题目】某精准扶贫帮扶单位,为帮助定点扶贫村真正脱贫,坚持扶贫同扶智相结合,帮助精准扶贫户利用互联网电商渠道销售当地特产苹果.苹果单果直径不同单价不同,为了更好的销售,现从该精准扶贫户种植的苹果树上随机摘下了50个苹果测量其直径,经统计,其单果直径分布在区间[50,95]内(单位:![]() ),统计的茎叶图如图所示:
),统计的茎叶图如图所示:

(Ⅰ)从单果直径落在[72,80)的苹果中随机抽取3个,求这3个苹果单果直径均小于76![]() 的概率;
的概率;
(Ⅱ)以此茎叶图中单果直径出现的频率代表概率.直径位于[65,90)内的苹果称为优质苹果,对于该精准扶贫户的这批苹果,某电商提出两种收购方案:
方案![]() :所有苹果均以5元/千克收购;
:所有苹果均以5元/千克收购;
方案![]() :从这批苹果中随机抽取3个苹果,若都是优质苹果,则按6元/干克收购;若有1个非优质苹果,则按5元/千克收购;若有2个非优质苹果,则按4.5元/千克收购;若有3个非优质苹果,则按4元/千克收购.
:从这批苹果中随机抽取3个苹果,若都是优质苹果,则按6元/干克收购;若有1个非优质苹果,则按5元/千克收购;若有2个非优质苹果,则按4.5元/千克收购;若有3个非优质苹果,则按4元/千克收购.
请你通过计算为该精准扶贫户推荐收益最好的方案.
查看答案和解析>>
科目:高中数学 来源: 题型:
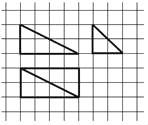
【题目】我国古代数学名著《九章算术商功》中阐述:“斜解立方,得两堑堵.斜解堑堵,其一为阳马,一为鳖臑.阳马居二,鳖臑居一,不易之率也.合两鳖臑三而一,验之以棊,其形露矣.”若称为“阳马”的某几何体的三视图如图所示,图中网格纸上小正方形的边长为1,对该几何体有如下描述:
①四个侧面都是直角三角形;
②最长的侧棱长为![]() ;
;
③四个侧面中有三个侧面是全等的直角三角形;
④外接球的表面积为24π.
其中正确的描述为____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设抛物线![]() :
:![]() 的焦点为
的焦点为![]() ,直线
,直线![]() 与
与![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() 的面积为
的面积为![]() .
.
(1)求![]() 的方程;
的方程;
(2)若![]() ,
,![]() 是
是![]() 上的两个动点,
上的两个动点,![]() ,试问:是否存在定点
,试问:是否存在定点![]() ,使得
,使得![]() ?若存在,求
?若存在,求![]() 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
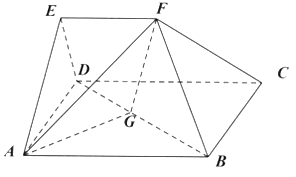
【题目】在多面体![]() 中,四边形
中,四边形![]() 是正方形,平面
是正方形,平面![]() 平面
平面![]() ,
,![]() .
.
(1)求证:![]() 平面
平面![]() ;
;
(2)在线段![]() 上是否存在点
上是否存在点![]() ,使得平面
,使得平面![]() 与平面
与平面![]() 所成的锐二面角的大小为
所成的锐二面角的大小为![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() O
O![]() 中,直线
中,直线![]() 与抛物线
与抛物线![]() =2
=2![]() 相交于A、B两点.
相交于A、B两点.
(1)求证:命题“如果直线![]() 过点T(3,0),那么
过点T(3,0),那么![]() =3”是真命题;
=3”是真命题;
(2)写出(1)中命题的逆命题,判断它是真命题还是假命题,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
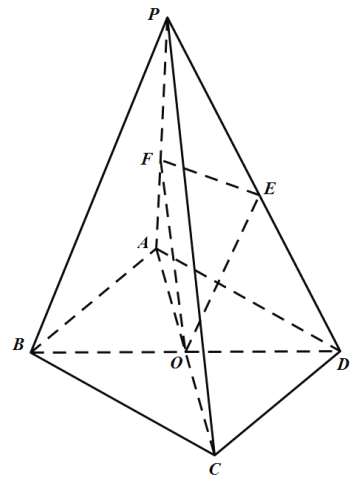
【题目】如图在四棱锥![]() 中,底面
中,底面![]() 为矩形,
为矩形,![]() ,
,![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() 为等腰直角三角形,且
为等腰直角三角形,且![]() ,
,![]() 为底面
为底面![]() 的中心.
的中心.
(1)求异面直线![]() 与
与![]() 所成角的余弦值;
所成角的余弦值;
(2)若![]() 为
为![]() 中点,
中点,![]() 在棱
在棱![]() 上,若
上,若![]() ,
,![]() ,且二面角
,且二面角![]() 的正弦值为
的正弦值为![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校高一年级学生某次身体素质体能测试的原始成绩采用百分制,已知所有这些学生的原始成绩均分布在![]() 内,发布成绩使用等级制各等级划分标准见下表,规定:
内,发布成绩使用等级制各等级划分标准见下表,规定: ![]() 、
、![]() 、
、![]() 三级为合格等级,
三级为合格等级, ![]() 为不合格等级.
为不合格等级.
百分制 |
|
|
|
|
等级 |
|
|
|
|
为了解该校高一年级学生身体素质情况,从中抽取了![]() 名学生的原始成绩作为样本进行统计,按照
名学生的原始成绩作为样本进行统计,按照![]() 的分组作出频率分布直方图如图
的分组作出频率分布直方图如图![]() 所示,样本中分数在
所示,样本中分数在![]() 分及以上的所有数据的茎叶图如图
分及以上的所有数据的茎叶图如图![]() 所示.
所示.
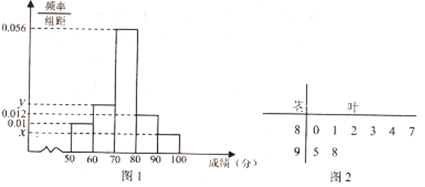
(1)求![]() 和频率分布直方图中的
和频率分布直方图中的![]() 的值;
的值;
(2)根据样本估计总体的思想,以事件发生的频率作为相应事件发生的概率,若在该校高一学生任选![]() 人,求至少有
人,求至少有![]() 人成绩是合格等级的概率;
人成绩是合格等级的概率;
(3)在选取的样本中,从![]() 、
、![]() 两个等级的学生中随机抽取了
两个等级的学生中随机抽取了![]() 名学生进行调研,记
名学生进行调研,记![]() 表示所抽取的
表示所抽取的![]() 名学生中为
名学生中为![]() 等级的学生人数,求随机变量
等级的学生人数,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中的真命题是( )
A. 若![]() ,则向量
,则向量![]() 与
与![]() 的夹角为钝角
的夹角为钝角
B. 若![]() ,则
,则![]()
C. 若命题“![]() 是真命题”,则命题“
是真命题”,则命题“![]() 是真命题”
是真命题”
D. 命题“![]() ,
,![]() ”的否定是“
”的否定是“![]() ,
,![]() ”
”
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com