
 内的点P(1,2)作两条互相垂直的弦AB,CD,若弦AB,CD的中点分别为M,N,则直线MN恒过定点,定点的坐标为 .
内的点P(1,2)作两条互相垂直的弦AB,CD,若弦AB,CD的中点分别为M,N,则直线MN恒过定点,定点的坐标为 . 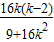 ,
,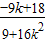 ),同样理得出N(
),同样理得出N( ,
, ),从而得到直线MN关于k为参数的两点式方程.分别取k=1和k=-1,得到动直线MN的两个位置,记为l1、l2,因为直线MN恒过定点,所以l1与l2的交点即为MN恒过的定点,由此联解直线l1与l2的方程组即可得到经过的定点坐标.
),从而得到直线MN关于k为参数的两点式方程.分别取k=1和k=-1,得到动直线MN的两个位置,记为l1、l2,因为直线MN恒过定点,所以l1与l2的交点即为MN恒过的定点,由此联解直线l1与l2的方程组即可得到经过的定点坐标. ,可得xM=
,可得xM= (x1+x2)=
(x1+x2)=
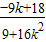
 ,
,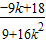 )
)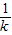 代替k,得CD中点为N(
代替k,得CD中点为N( ,
,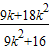 )
)
 ,记为l1; 再k=-1,得直线方程
,记为l1; 再k=-1,得直线方程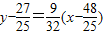 ,记为l2.
,记为l2.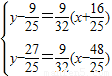 ,得
,得
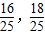 )
)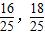 )
)

科目:高中数学 来源: 题型:
| x2 |
| 16 |
| y2 |
| 9 |
| 16 |
| 25 |
| 18 |
| 25 |
| 16 |
| 25 |
| 18 |
| 25 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
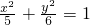 内的一点P(-1,2)的弦,恰好被P点平分,则这条弦所在的直线方程为
内的一点P(-1,2)的弦,恰好被P点平分,则这条弦所在的直线方程为查看答案和解析>>
科目:高中数学 来源:2010-2011学年福建省泉州一中高三(上)期末数学试卷(文科)(解析版) 题型:选择题
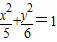 内的一点P(-1,2)的弦,恰好被P点平分,则这条弦所在的直线方程为( )
内的一点P(-1,2)的弦,恰好被P点平分,则这条弦所在的直线方程为( )查看答案和解析>>
科目:高中数学 来源: 题型:
过椭圆![]() 内的一点P(-1,2)的弦,恰好被P点平分,则这条弦所在的直线方程为 ( )
内的一点P(-1,2)的弦,恰好被P点平分,则这条弦所在的直线方程为 ( )
A.3x-5y+13=0 B.3x+5y+13=0 C.5x-3y+11=0 D.5x+3y+11=0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com