
【题目】为方便市民休闲观光,市政府计划在半径为200米,圆心角为![]() 的扇形广场内(如图所示),沿
的扇形广场内(如图所示),沿![]() 边界修建观光道路,其中
边界修建观光道路,其中![]() 分别在线段
分别在线段![]() 上,且
上,且![]() 两点间距离为定长
两点间距离为定长![]() 米.
米.
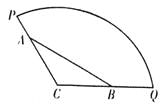
(1)当![]() 时,求观光道
时,求观光道![]() 段的长度;
段的长度;
(2)为提高观光效果,应尽量增加观光道路总长度,试确定图中![]() 两点的位置,使观光道路总长度达到最长?并求出总长度的最大值.
两点的位置,使观光道路总长度达到最长?并求出总长度的最大值.
科目:高中数学 来源: 题型:
【题目】某校从高二年级学生中随机抽取50名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100],得到如图所示的频率分布直方图.
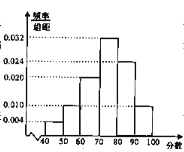
(1)若该校高二年级共有学生1000人,试估计成绩不低于60分的人数;
(2)求该校高二年级全体学生期中考试成绩的众数、中位数和平均数的估计值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有编号分别为1,2,3,4,5的五道不同的政治题和编号分别为6,7,8,9的四道不同的历史题.甲同学从这九道题中一次性随机抽取两道题,每道题被抽到的概率是相等的,用符号(x,y)表示事件“抽到的两道题的编号分别为x,y,且x<y.”.
(1)问有多少个基本事件,并列举出来;
(2)求甲同学所抽取的两道题的编号之和小于17但不小于11的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2+bx(a≠0)的导函数f′(x)=-2x+7,数列{an}的前n项和为Sn,点Pn(n,Sn)(n∈N*)均在函数y=f(x)的图象上,求数列{an}的通项公式及Sn的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两位数学老师组队参加某电视台闯关节目,共3关,甲作为嘉宾参与答题,若甲回答错误,乙作为亲友团在整个通关过程中至多只能为甲提供一次帮助机会,若乙回答正确,则甲继续闯关,若某一关通不过,则收获前面所有累积奖金.约定每关通过得到奖金2000元,设甲每关通过的概率为![]() ,乙每关通过的概率为
,乙每关通过的概率为![]() ,且各关是否通过及甲、乙回答正确与否均相互独立.
,且各关是否通过及甲、乙回答正确与否均相互独立.
(1)求甲、乙获得2000元奖金的概率;
(2)设![]() 表示甲、乙两人获得的奖金数,求随机变量
表示甲、乙两人获得的奖金数,求随机变量![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数![]() 的对称轴为
的对称轴为![]() ,
,![]() .
.
(1)求函数![]() 的最小值及取得最小值时
的最小值及取得最小值时![]() 的值;
的值;
(2)试确定![]() 的取值范围,使
的取值范围,使![]() 至少有一个实根;
至少有一个实根;
(3)当![]() 时,
时,![]() ,对任意
,对任意![]() 有
有![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】网络购物已经被大多数人接受,随着时间的推移,网络购物的人越来越多,然而也有部分人对网络购物的质量和信誉产生怀疑。对此,某新闻媒体进行了调查,在所有参与调查的人中,持“支持”和“不支持”态度的人数如下表所示:
年龄 态度 | 支持 | 不支持 |
20岁以上50岁以下 | 800 | 200 |
50岁以 (含50岁) | 100 | 300 |
(1)在所有参与调查的人中,用分层抽样的方法抽取![]() 个人,已知从持“支持”态度的人中抽取了9人,求
个人,已知从持“支持”态度的人中抽取了9人,求![]() 的值;
的值;
(2)是否有99.9%的把握认为支持网络购物与年龄有关?
参考数据:
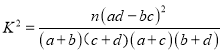 ,其中
,其中![]() ,
,
| 0.05 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com