
【题目】已知两个定点![]() ,动点
,动点![]() 满足
满足![]() .设动点
.设动点![]() 的轨迹为曲线
的轨迹为曲线![]() ,直线
,直线![]() .
.
(1)求曲线![]() 的轨迹方程;
的轨迹方程;
(2)若![]() 与曲线
与曲线![]() 交于不同的
交于不同的![]() 两点,且
两点,且![]() (
(![]() 为坐标原点),求直线
为坐标原点),求直线![]() 的斜率;
的斜率;
(3)若![]() 是直线
是直线![]() 上的动点,过
上的动点,过![]() 作曲线
作曲线![]() 的两条切线
的两条切线![]() ,切点为
,切点为![]() ,探究:直线
,探究:直线![]() 是否过定点.
是否过定点.
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣ ![]() (a>0)
(a>0)
(1)若函数f(x)在x=2处的切线与x轴平行,求实数a的值;
(2)讨论函数f(x)在区间[1,2]上的单调性;
(3)证明: ![]() >e.
>e.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在实数集R中定义一种运算“*”,对任意给定的a,b∈R,a*b为唯一确定的实数,且具有性质: ⑴对任意a,b∈R,a*b=b*a;(2)对任意a∈R,a*0=a;(3)对任意a,b∈R,(a*b)*c=c*(ab)+(a*c)+(c*b)﹣2c.关于函数f(x)=(3x)* ![]() 的性质,有如下说法:
的性质,有如下说法:
①函数f(x)的最小值为3;
②函数f(x)为奇函数;
③函数f(x)的单调递增区间为(﹣∞,﹣ ![]() ),(
),( ![]() ,+∞).
,+∞).
其中所有正确说法的个数为( )
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直四棱柱![]() 中,底面
中,底面![]() 是边长为2的正方形,
是边长为2的正方形, ![]() 分别为线段
分别为线段![]() ,
, ![]() 的中点.
的中点.
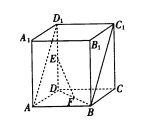
(1)求证: ![]() ||平面
||平面![]() ;
;
(2)四棱柱![]() 的外接球的表面积为
的外接球的表面积为![]() ,求异面直线
,求异面直线![]() 与
与![]() 所成的角的大小.
所成的角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本题满分16分)某批发公司批发某商品,每件商品进价80元,批发价120元,该批发商为鼓励经销商批发,决定当一次批发量超过100个时,每多批发一个,批发的全部商品的单价就降低0.04元,但最低批发价不能低于102元.
(1)当一次订购量为多少个时,每件商品的实际批发价为102元?
(2)当一次订购量为![]() 个, 每件商品的实际批发价为
个, 每件商品的实际批发价为![]() 元,写出函数
元,写出函数![]() 的表达式;
的表达式;
(3)根据市场调查发现,经销商一次最大定购量为![]() 个,则当经销商一次批发多少个零件时,该批发公司可获得最大利润.
个,则当经销商一次批发多少个零件时,该批发公司可获得最大利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市由甲、乙两家乒乓球俱乐部,两家设备和服务都很好,但收费方式不同,甲家每张球台每小时5元;乙家按月计费,一个月中![]() 小时以内(含
小时以内(含![]() 小时)每张球台
小时)每张球台![]() 元,超过
元,超过![]() 小时的部分每张球台每小时
小时的部分每张球台每小时![]() 元.某公司准备下个月从两家中的一家租一张球台开展活动,活动时间不少于
元.某公司准备下个月从两家中的一家租一张球台开展活动,活动时间不少于![]() 小时,也不超过
小时,也不超过![]() 小时,设在甲家租一张球台开展活动
小时,设在甲家租一张球台开展活动![]() 小时的收费为
小时的收费为![]() 元,在乙家租一张球台开展活动
元,在乙家租一张球台开展活动![]() 小时的收费为
小时的收费为![]() 元.
元.
(1)试分别写出![]() 与
与![]() 的解析式;
的解析式;
(2)选择哪家比较合算?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com