Question

17．地球的北纬45°圈上有A，B两点，它们分别在东经70°和东经160°的经线上，则A，B两点的球面距离与其在此北纬45°圈上劣弧长的比值为$\frac{3\sqrt{2}}{4}$．

Answer 1

分析 由于A、B两地在同一纬度圈上，可以先计算出它们的经度差和45°的纬圆半径，再求出A、B两地对应的AB弦长，以及球心角，求出A、B两点在纬度圈上的劣弧长、球面距离，即可得到结论．

解答 解：设北纬45°圈的半径为r，
∵点A在东经70°处，点B在东经160°处，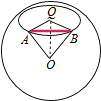

∴甲、乙两地对应点的纬圆半径是r=Rcos45°=$\frac{\sqrt{2}}{2}$R，经度差是90°，
∴A、B两点在纬度圈上的劣弧长为$\frac{\sqrt{2}}{4}$πR，
∵AB=$\sqrt{2}$r=R，
∴∠AOB=$\frac{π}{3}$，
∴A、B两点的球面距离为$\frac{1}{3}$πR，
∴A、B两点在纬度圈上的劣弧长与A、B两点的球面距离之比是$\frac{\frac{\sqrt{2}}{4}πR}{\frac{1}{3}πR}$=$\frac{3\sqrt{2}}{4}$，
故答案为：$\frac{3\sqrt{2}}{4}$．

点评 本题主要考查了球面距离及相关计算，考查空间想象力，属于中档题