

图7
活动:平面向量基本定理是平面向量的重要定理,它是解决平面向量计算问题的重要工具.由平面向量基本定理,可得到下面两个推论:
推论1:e1与e2是同一平面内的两个不共线向量,若存在实数λ1、λ2,使得λ1e1+λ2e2=0,则λ1=λ2=0.
推论2:e1与e2是同一平面内的两个不共线向量,若存在实数a.1,a.2,b1,b2,使得a=a1e1+a2e2=b1e1+b2e2,则
解:∵![]() =
=![]() +
+![]() ,
,![]() =
=![]() +
+![]() ,
,
∴由![]() +2
+2![]() +3
+3![]() =0,得(
=0,得(![]() +
+![]() )+2(
)+2(![]() +
+![]() )+3
)+3![]() =0.
=0.
∴![]() +3
+3![]() +2
+2![]() +3
+3![]() =0.又∵A.、N、B三点共线,C、M、N三点共线,
=0.又∵A.、N、B三点共线,C、M、N三点共线,
由平行向量基本定理,设![]() =λ
=λ![]() ,
,![]() =μ
=μ![]() ,
,
∴λ![]() +3
+3![]() +2
+2![]() +3μ
+3μ![]() =0.∴(λ+2)
=0.∴(λ+2)![]() +(3+3μ)
+(3+3μ)![]() =0.
=0.
由于![]() 和
和![]() 不共线,∴
不共线,∴![]() .∴
.∴![]()
∴![]() =-
=-![]() =
=![]() .∴
.∴![]() =
=![]() +
+![]() =2
=2![]() =2a.
=2a.
点评:这里选取![]() ,
,![]() 作为基底,运用化归思想,把问题归结为λ1e1+λ2e2=0的形式来解决.
作为基底,运用化归思想,把问题归结为λ1e1+λ2e2=0的形式来解决.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
 [选做题]本题包括A、B、C、D共4小题,请从这4小题中选做2小题,每小题10分,共20分.
[选做题]本题包括A、B、C、D共4小题,请从这4小题中选做2小题,每小题10分,共20分.
|
| π |
| 4 |
|
查看答案和解析>>
科目:高中数学 来源: 题型:
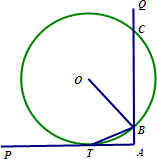 (1)如图,∠PAQ是直角,圆O与AP相切于点T,与AQ相交于两点B,C.求证:BT平分∠OBA
(1)如图,∠PAQ是直角,圆O与AP相切于点T,与AQ相交于两点B,C.求证:BT平分∠OBA
|
查看答案和解析>>
科目:高中数学 来源: 题型:
 本题包括(1)、(2)、(3)、(4)四小题,请选定其中两题,并在答题卡指定区域内答,
本题包括(1)、(2)、(3)、(4)四小题,请选定其中两题,并在答题卡指定区域内答,
|
查看答案和解析>>
科目:高中数学 来源:2012-2013学年山东省高三第三次(3月)周测文科数学试卷(解析版) 题型:选择题
如图,AB是圆O的直径,P是圆弧 上的点,M,N是直径AB上关于O对称的两点,且
上的点,M,N是直径AB上关于O对称的两点,且 ,则
,则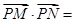

A.13 B.7 C.5 D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com