
已知函数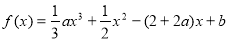 (
(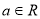 )
)
(1)若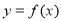 在点
在点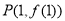 处的切线方程为
处的切线方程为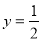 ,求
,求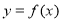 的解析式及单调递减区间;
的解析式及单调递减区间;
(2)若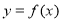 在
在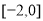 上存在极值点,求实数
上存在极值点,求实数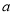 的取值范围.
的取值范围.
(1) ,单调递减区间有
,单调递减区间有 ;(2)
;(2)
【解析】
试题分析:(1)由题设知,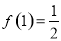 ,
,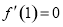 解方程组可得
解方程组可得 的值,进而确定函数
的值,进而确定函数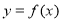 的解析式及其导数的表达式
的解析式及其导数的表达式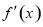 ,并由不等式
,并由不等式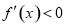 的解得到函数据的单调递减区间.
的解得到函数据的单调递减区间.
(2)函数 在
在 上存在极值点
上存在极值点 导函数
导函数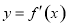 在
在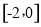 上存在零点,且零点两侧导数值异号,因为,导函数的二次项系数为
上存在零点,且零点两侧导数值异号,因为,导函数的二次项系数为 ,所以要分
,所以要分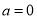 与
与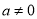 两种情詋进行讨论,后者为一元二次方程的分布问题.
两种情詋进行讨论,后者为一元二次方程的分布问题.
试题解析: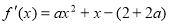
(1)由已知可得
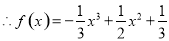
此时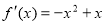 , 4分
, 4分
由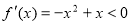 得
得 的单调递减区间为
的单调递减区间为 ; 7分
; 7分
(2)由已知可得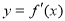 在
在 上存在零点且在零点两侧
上存在零点且在零点两侧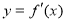 值异号
值异号
⑴ 时,
时,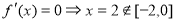 ,不满足条件;
,不满足条件;
⑵ 时,可得
时,可得 在
在 上有解且
上有解且
设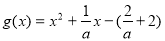
①当 时,满足
时,满足 在
在 上有解
上有解
 或
或 此时满足
此时满足
②当 时,即
时,即 在
在 上有两个不同的实根
上有两个不同的实根
则
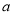 无解
无解
综上可得实数 的取值范围为
的取值范围为 . 14分
. 14分
考点:1、导数的几何意;2、导数在研究函数单调性与极值等性质中的应用;3、二次函数与一元二次方程.


科目:高中数学 来源:2013-2014学年安徽省“江淮十校协作体”四月联考卷文科数学试卷(解析版) 题型:解答题
以下茎叶图记录了甲,乙两组各三名同学在期末考试中的数学成绩(十位数字为茎,个位数字为叶).乙组记录中有一个数字模糊,无法确认,假设这个数字具有随机性,并在图中以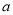 表示.
表示.
(1)若甲,乙两个小组的数学平均成绩相同,求 的值;
的值;
(2)当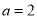 时,分别从甲,乙两组同学中各随机选取一名同学,求这两名同学的数学成绩之差的绝对值不超过2分的概率.
时,分别从甲,乙两组同学中各随机选取一名同学,求这两名同学的数学成绩之差的绝对值不超过2分的概率.

查看答案和解析>>
科目:高中数学 来源:2013-2014学年安徽省“江南十校”高三第二次模拟考试文科数学试卷(解析版) 题型:选择题
已知等差数列 和等比数列
和等比数列 满足:
满足: ,且
,且 ,则
,则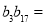 ( )
( )
A.9 B.12 C.16 D.36
查看答案和解析>>
科目:高中数学 来源:2013-2014学年天津市蓟县高三第一次模拟考试理科数学试卷(解析版) 题型:填空题
若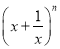 展开式的二项式系数之和为256,则
展开式的二项式系数之和为256,则 =_________,其展开式的常数项等于__________。(用数字作答)
=_________,其展开式的常数项等于__________。(用数字作答)
查看答案和解析>>
科目:高中数学 来源:2013-2014学年天津市蓟县高三第一次模拟考试理科数学试卷(解析版) 题型:选择题
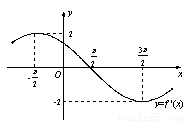
已知函数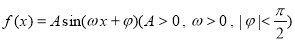 ,其导函数
,其导函数 的部分图象如图所示,则函数
的部分图象如图所示,则函数 的解析式为( )
的解析式为( )
A.
B.
C.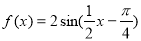
D.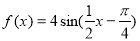
查看答案和解析>>
科目:高中数学 来源:2013-2014学年天津市蓟县高三第一次模拟考试文科数学试卷(解析版) 题型:选择题
已知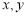 满足
满足 ,记目标函数
,记目标函数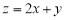 的最大值为
的最大值为 ,最小值为
,最小值为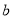 ,则
,则
A.1 B.2 C.7 D.8
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com