
分析 (1)求出f(x)的导数,由条件列方程,可得b=9,c=1,由a>0,令导数大于0,可得增区间;令导数小于0,可得减区间;
(2)当x>1时,(x3+1)f(x)>9+lnx.即为f(x)>$\frac{9+lnx}{1+{x}^{3}}$在x>1成立,分别求得f(x)的最值和g(x)=$\frac{9+lnx}{1+{x}^{3}}$的最值,即可得证.
解答 (1)解:f(x)=$\frac{bx}{a{x}^{2}+c}$,
f'(x)=$\frac{-ab{x}^{2}+9}{(a{x}^{2}+1)^{2}}$,f′(0)=9,且b+c=10,
∴c=1,b=9,f'(x)=$\frac{-9a{x}^{2}+9}{(a{x}^{2}+1)^{2}}$,a>0,
当x∈(-$\frac{\sqrt{a}}{a}$,$\frac{\sqrt{a}}{a}$)时,f'(x)>0,f(x)递增;
当x∈(-∞,-$\frac{\sqrt{a}}{a}$)和($\frac{\sqrt{a}}{a}$,+∞)时,f'(x)<0,f(x)递减;
(2)证明:当x>1时,(x3+1)f(x)>9+lnx.即为f(x)>$\frac{9+lnx}{1+{x}^{3}}$在x>1成立,
由g(x)=$\frac{9+lnx}{1+{x}^{3}}$的导数为g'(x)=$\frac{\frac{1}{x}-26{x}^{2}-3{x}^{2}lnx}{(1+{x}^{3})^{2}}$<0,
即有g(x)在x>1递减,则g(x)<g(1)=$\frac{9}{2}$;
由(1)可得f(x)在(1,$\frac{\sqrt{a}}{a}$)时,f(x)递增;
($\frac{\sqrt{a}}{a}$,+∞)时,f(x)递减.
x=1时f(1)=$\frac{9}{1+a}$≥$\frac{9}{2}$,
可得x=$\frac{1}{\sqrt{a}}$处取得最大值,即为$\frac{9}{2\sqrt{a}}$>$\frac{9}{2}$,
又($\frac{\sqrt{a}}{a}$,+∞)时,f(x)>g(x).
则有当x>1时,(x3+1)f(x)>9+lnx.
点评 本题考查导数的运用:求单调区间和极值、最值,考查不等式的恒成立问题的解法,注意运用函数的导数求得单调性,考查运算能力,属于中档题.


 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:高中数学 来源: 题型:解答题
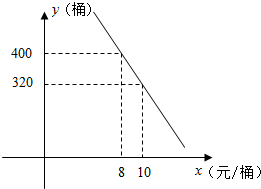 高一某班共有学生43人,据统计原来每人每年用于购买饮料的平均支出是120元.若该班全体学生改饮某品牌的桶装纯净水,经测算和市场调查,其年总费用由两部分组成,一部分是购买纯净水的费用,另一部分是其它费用260元,其中,纯净水的销售价x(元/桶)与年购买总量y(桶)之间满足如图直线所示关系.
高一某班共有学生43人,据统计原来每人每年用于购买饮料的平均支出是120元.若该班全体学生改饮某品牌的桶装纯净水,经测算和市场调查,其年总费用由两部分组成,一部分是购买纯净水的费用,另一部分是其它费用260元,其中,纯净水的销售价x(元/桶)与年购买总量y(桶)之间满足如图直线所示关系.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(\frac{1}{3},1)$ | B. | $(-\frac{1}{3},-\frac{1}{4})$ | C. | $(\frac{1}{3},1)∪(-1,-\frac{1}{3})$ | D. | $(-\frac{1}{3},-\frac{1}{4})∪(\frac{1}{4},\frac{1}{3})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,2) | B. | (-2,$\frac{9}{4}$) | C. | (-$\frac{9}{4}$,$\frac{9}{4}$) | D. | $(-\frac{9}{4},2)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(0,\frac{1}{3})$ | B. | $(\frac{1}{3},\frac{1}{2})$ | C. | $(\frac{1}{2},\frac{2}{3})$ | D. | $(\frac{2}{3},1)$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com