练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】在平面直角坐标系中，P为直线：上的动点，动点Q满足，且原点O在以为直径的圆上.记动点Q的轨迹为曲线C

    （1）求曲线C的方程：

    （2）过点的直线与曲线C交于A，B两点，点D（异于A，B）在C上，直线，分别与x轴交于点M，N，且，求面积的最小值.

    【答案】（1）（2）

    【解析】

    （1）设动点，表示出，再由原点O在以为直径的圆上，转化为，得到曲线C的方程.

    （2）设而不解，利用方程思想、韦达定理构建面积的函数关系式，再求最小值.

    解：（1）由题意，不妨设，则，，

    ∵O在以为直径的圆上，∴，∴，

    ∴，∴曲线C的方程为.

    （2）设，，，，，

    依题意，可设：（其中），由方程组消去x并整理，得

    ，则，，

    同理可设，，

    可得，，

    ∴，，

    又∵，∴，

    ∴，∴，

    ∴

    ，

    ∴，

    ∴当时，面积取得最小值，其最小值为.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数．

    （1）函数在内有两个不同零点，求的取值范围；

    （2）在第（1）问的条件下判断当时，曲线是否位于轴下方，并说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】东莞的轻轨给市民出行带来了很大的方便，越来越多的市民选择乘坐轻轨出行，很多市民都会开汽车到离家最近的轻轨站，将车停放在轻轨站停车场，然后进站乘轻轨出行，这给轻轨站停车场带来很大的压力.某轻轨站停车场为了解决这个问题，决定对机动车停车施行收费制度，收费标准如下:4小时内(含4小时)每辆每次收费5元；超过4小时不超过6小时，每增加一小时收费增加3元；超过6小时不超过8小时，每增加一小时收费增加4元，超过8小时至24小时内(含24小时)收费30元；超过24小时，按前述标准重新计费.上述标准不足一小时的按一小时计费.为了调查该停车场一天的收费情况，现统计1000辆车的停留时间(假设每辆车一天内在该停车场仅停车一次)，得到下面的频数分布表:

    以车辆在停车场停留时间位于各区间的频率代替车辆在停车场停留时间位于各区间的概率.

    (1)现在用分层抽样的方法从上面1000辆车中抽取了100辆车进行进一步深入调研，记录并统计了停车时长与司机性别的列联表:

    完成上述列联表，并判断能否有的把握认为“停车是否超过6小时”与性别有关?

    (2)(i)X表示某辆车一天之内(含一天)在该停车场停车一次所交费用，求X的概率分布列及期望:

    (ii)现随机抽取该停车场内停放的3辆车，表示3辆车中停车费用大于的车辆数，求P()的概率.

    参考公式: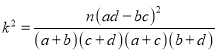，其中

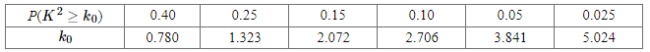
    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某企业引进现代化管理体制，生产效益明显提高，2019年全年总收入与2018年全年总收入相比增长了一倍，同时该企业的各项运营成本也随着收入的变化发生相应变化，下图给出了该企业这两年不同运营成本占全年总收入的比例，下列说法错误的是（ ）

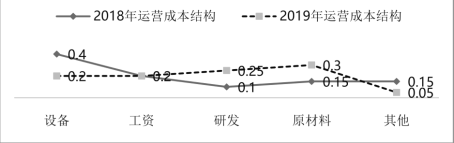
    A.该企业2019年研发的费用与原材料的费用超过当年总收入的50%

    B.该企业2019年设备支出金额及原材料的费用均与2018相当

    C.该企业2019年工资支出总额比2018年多一倍

    D.该企业2018年与2019研发的总费用占这两年总收入的20%

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】近年来，国家为了鼓励高校毕业生自主创业，出台了许多优惠政策，以创业带动就业．某高校毕业生小李自主创业从事海鲜的批发销售，他每天以每箱300元的价格购入基围虾，然后以每箱500元的价格出售，如果当天购入的基围虾卖不完，剩余的就作垃圾处理．为了对自己的经营状况有更清晰的把握，他记录了150天基围虾的日销售量（单位：箱），制成如图所示的频数分布条形图．

    （1）若小李一天购进12箱基围虾．

    ①求当天的利润（单位：元）关于当天的销售量（单位：箱，）的函数解析式；

    ②以这150天记录的日销售量的频率作为概率，求当天的利润不低于1900元的概率；

    （2）以上述样本数据作为决策的依据，他计划今后每天购进基围虾的箱数相同，并在进货量为11箱，12箱中选择其一，试帮他确定进货的方案，以使其所获的日平均利润最大．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在中，，，有下述四个结论：

    ①若为的重心，则

    ②若为边上的一个动点，则为定值2

    ③若，为边上的两个动点，且，则的最小值为

    ④已知为内一点，若，且，则的最大值为2

    其中所有正确结论的编号是（ ）

    A.①③B.①④C.②③D.②④

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在等差数列中，已知公差， ，且， ， 成等比数列.

    （1）求数列的通项公式；

    （2）求.

    【答案】（1）；（2）100

    【解析】试题分析：（1）根据题意， ， 成等比数列得得求出d即可得通项公式；（2）求项的绝对前n项和，首先分清数列有多少项正数项和负数项，然后正数项绝对值数值不变，负数项绝对值要变号，从而得，得，由，得，∴ 计算 即可得出结论

    解析：（1）由题意可得，则， ，

    ，即，

    化简得，解得或（舍去）.

    ∴.

    （2）由（1）得时，

    由，得，由，得，

    ∴

    .

    ∴.

    点睛：对于数列第一问首先要熟悉等差和等比通项公式及其性质即可轻松解决，对于第二问前n项的绝对值的和问题，首先要找到数列由多少正数项和负数项，进而找到绝对值所影响的项，然后在求解即可得结论

    【题型】解答题
    【结束】
    18

    【题目】甲、乙两家销售公司拟各招聘一名产品推销员，日工资方案如下: 甲公司规定底薪80元，每销售一件产品提成1元; 乙公司规定底薪120元，日销售量不超过45件没有提成，超过45件的部分每件提成8元.

    (I)请将两家公司各一名推销员的日工资 (单位: 元) 分别表示为日销售件数的函数关系式;

    (II)从两家公司各随机选取一名推销员，对他们过去100天的销售情况进行统计，得到如下条形图。若记甲公司该推销员的日工资为,乙公司该推销员的日工资为 (单位: 元)，将该频率视为概率，请回答下面问题:

    某大学毕业生拟到两家公司中的一家应聘推销员工作，如果仅从日均收入的角度考虑，请你利用所学的统计学知识为他作出选择，并说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某中学高二年级组织外出参加学业水平考试，出行方式为：乘坐学校定制公交或自行打车前往，大数据分析显示，当的学生选择自行打车，自行打车的平均时间为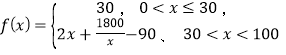 (单位:分钟) ,而乘坐定制公交的平均时间不受影响,恒为40分钟,试根据上述分析结果回答下列问题:

    （1）当在什么范围内时,乘坐定制公交的平均时间少于自行打车的平均时间?

    （2）求该校学生参加考试平均时间的表达式:讨论的单调性,并说明其实际意义.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在正方体中，点是线段上的动点，以下结论：

    ①平面；

    ②；

    ③三棱锥，体积不变；

    ④为中点时，直线与平面所成角最大.

    其中正确的序号为（ ）

    A.①④B.②④C.①②③D.①②③④

    查看答案和解析>>

    同步练习册答案