
分析 (Ⅰ)设“从甲盒内取出的2个球均为黑球”为事件A,“从乙盒内取出的2个球均为黑球”为事件B.且AB独立,由独立事件的概率公式可得;
(Ⅱ)设“从甲盒内取出的2个球均为黑球;从乙盒内取出的2个球中,1个是红球,1个是黑球”为事件C,“从甲盒内取出的2个球中,1个是红球,1个是黑球;从乙盒内取出的2个球均为黑球”为事件D.由互斥事件的概率公式可得答案.
(Ⅲ)ξ为取出的4个球中红球的个数,则ξ可能的取值为0,1,2,3.结合前两问的解法得到结果,写出分布列和期望.
解答 解:(I)设“从甲盒内取出的2个球均为黑球”为事件A,“从乙盒内取出的2个球均为黑球”为事件B.
∵事件A,B相互独立,且$P(A)=\frac{{C}_{3}^{2}}{{C}_{4}^{2}}=\frac{1}{2}$,$P(B)=\frac{{C}_{3}^{2}}{{C}_{5}^{2}}=\frac{3}{10}$.
∴取出的4个球均为黑球的概率为P(A•B)=P(A)•P(B)=$\frac{1}{2}$×$\frac{3}{10}$=$\frac{3}{20}$.
(II)设“从甲盒内取出的2个球均为黑球;从乙盒内取出的2个球中,1个是红球,1个是黑球”为事件C,
“从甲盒内取出的2个球中,1个是红球,1个是黑球;从乙盒内取出的2个球均为黑球”为事件D.
∵事件C,D互斥,且$P(C)=\frac{{C}_{3}^{2}}{{C}_{4}^{2}}•\frac{{C}_{3}^{1}•{C}_{2}^{1}}{{C}_{5}^{2}}=\frac{3}{10}$.$P(D)=\frac{{C}_{3}^{1}}{{C}_{4}^{2}}•\frac{{C}_{3}^{2}}{{C}_{5}^{2}}=\frac{3}{20}$,
∴取出的4个球中恰有1个红球的概率为P(C+D)=P(C)+P(D)=$\frac{3}{10}+\frac{3}{20}$=$\frac{9}{20}$.
(III)ξ可能的取值为0,1,2,3.
由(I),(II)得P(ξ=0)=$\frac{3}{20}$,P(ξ=1)=$\frac{9}{20}$,
又P(ξ=2)=$\frac{{C}_{3}^{2}}{{C}_{4}^{2}}•\frac{{C}_{3}^{1}•{C}_{2}^{1}}{{C}_{5}^{2}}+\frac{{C}_{3}^{2}}{{C}_{4}^{2}}•\frac{{C}_{2}^{2}}{{C}_{5}^{2}}=\frac{7}{20}$,
P(ξ=3)=$\frac{{C}_{3}^{2}}{{C}_{4}^{2}}•\frac{{C}_{2}^{2}}{{C}_{5}^{2}}$=$\frac{1}{20}$.
ξ的分布列为:
| ξ | 0 | 1 | 2 | 3 |
| P | $\frac{3}{20}$ | $\frac{9}{20}$ | $\frac{7}{20}$ | $\frac{1}{20}$ |
点评 本小题主要考查互斥事件、相互独立事件、离散型随机变量的分布列和数学期望等基础知识,考查运用概率知识解决实际问题的能力.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,1) | B. | (-1,1) | C. | (1,3) | D. | (-∞,-l) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 35x5 | B. | 35x2 | C. | 35x5和-35x5 | D. | -35x5和35x2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
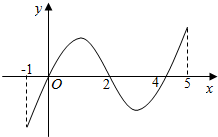 已知函数f(x)的定义域为[-1,5],部分对应值如表,f(x)的导函数y=f′(x)的图象如图所示.下列四个命题:
已知函数f(x)的定义域为[-1,5],部分对应值如表,f(x)的导函数y=f′(x)的图象如图所示.下列四个命题:| x | -1 | 0 | 4 | 5 |
| f(x) | -1 | -2 | -2 | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com