
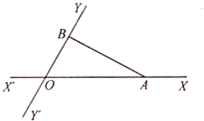
 如图,有两条相交成60°角的直路XX′,YY′,交点是O,甲和乙同时从点O出发,甲沿着OX的方向,乙沿着OY的方向,经过若干小时后,甲到达点A,乙到达点B,此时甲测得他走过的路程比他到乙的距离多2km,且乙走过的路程超过4km,设甲到达点A,乙到达点B时,乙走过的路程为x km,甲走过的路程为y km.
如图,有两条相交成60°角的直路XX′,YY′,交点是O,甲和乙同时从点O出发,甲沿着OX的方向,乙沿着OY的方向,经过若干小时后,甲到达点A,乙到达点B,此时甲测得他走过的路程比他到乙的距离多2km,且乙走过的路程超过4km,设甲到达点A,乙到达点B时,乙走过的路程为x km,甲走过的路程为y km.分析 (1)在△OAB中由余弦定理得(y-2)2=y2+x2-2xycos60°(x>4)整理即可得函数关系式.
(2)由题意S=x+y=$\frac{2{x}^{2}-4x-4}{x-4}$,设t=x-4,则x=t+4,其中t>0,利用基本不等式的应用即可求解.
解答 解:(1)在△OAB中,由余弦定理得(y-2)2=y2+x2-2xycos60° (x>4),…(3分)
整理得,y=$\frac{{x}^{2}-4}{x-4}$(x>4).…(6分)
(2)由题意S=x+y=x+$\frac{{x}^{2}-4}{x-4}$=$\frac{2{x}^{2}-4x-4}{x-4}$,…(8分)
设t=x-4,则x=t+4,其中t>0,…(10分)
S=$\frac{2(t+4)^{2}-4(t+4)-4}{t}$
=2(t+$\frac{6}{t}$)+12 …(13分)
≥4$\sqrt{6}$+12.当且仅当t=$\sqrt{6}$时取等号,此时x=4+$\sqrt{6}$,…(15分)
S的最小值是4$\sqrt{6}$+12. …(16分)
点评 本题主要考查了余弦定理,基本不等式的应用,考查了计算能力和转化思想,属于中档题.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
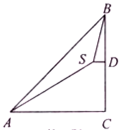 如图,在山底A处测得山顶B的仰角∠CAB=45°,沿倾斜角为30°的斜坡AS走2000米至S点,又测得山顶∠DSB=75°,则山高BC为2000米.
如图,在山底A处测得山顶B的仰角∠CAB=45°,沿倾斜角为30°的斜坡AS走2000米至S点,又测得山顶∠DSB=75°,则山高BC为2000米.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,2) | B. | (2,3) | C. | (1,2)或(2,3) | D. | 不能确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com