
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,已知cosC+(cosA﹣ ![]() sinA)cosB=0.
sinA)cosB=0.
(1)求角B的大小;
(2)若a+c=1,求b的取值范围.
【答案】
(1)解:由已知得:﹣cos(A+B)+cosAcosB﹣ ![]() sinAcosB=0,
sinAcosB=0,
即sinAsinB﹣ ![]() sinAcosB=0,
sinAcosB=0,
∵sinA≠0,∴sinB﹣ ![]() cosB=0,即tanB=
cosB=0,即tanB= ![]() ,
,
又B为三角形的内角,
则B= ![]()
(2)解:∵a+c=1,即c=1﹣a,cosB= ![]() ,
,
∴由余弦定理得:b2=a2+c2﹣2accosB,即b2=a2+c2﹣ac=(a+c)2﹣3ac=1﹣3a(1﹣a)=3(a﹣ ![]() )2+
)2+ ![]() ,
,
∵0<a<1,∴ ![]() ≤b2<1,
≤b2<1,
则 ![]() ≤b<1
≤b<1
【解析】(1)已知等式第一项利用诱导公式化简,第二项利用单项式乘多项式法则计算,整理后根据sinA不为0求出tanB的值,由B为三角形的内角,利用特殊角的三角函数值即可求出B的度数;(2)由余弦定理列出关系式,变形后将a+c及cosB的值代入表示出b2 , 根据a的范围,利用二次函数的性质求出b2的范围,即可求出b的范围.
【考点精析】本题主要考查了两角和与差的余弦公式和余弦定理的定义的相关知识点,需要掌握两角和与差的余弦公式:![]() ;余弦定理:
;余弦定理:![]() ;
;![]() ;
;![]() 才能正确解答此题.
才能正确解答此题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图所示,在三棱锥P﹣ABQ中,PB⊥平面ABQ,BA=BP=BQ,D,C,E,F分别是AQ,BQ,AP,BP的中点,AQ=2BD,PD与EQ交于点G,PC与FQ交于点H,连接GH. 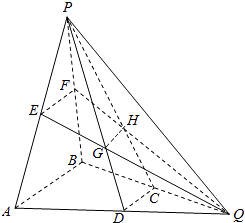
(1)求证:AB∥GH;
(2)求二面角D﹣GH﹣E的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】 已知函数f(x)=ax3+bx2的图象经过点M(1,4),曲线在点M处的切线恰好与直线x+9y﹣3=0垂直.
(1)求实数a、b的值
(2)若函数f(x)在区间[m,m+1]上单调递增,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,半径为1的半圆O与等边三角形ABC夹在两平行线l1 , l2之间,l∥l1 , l与半圆相交于F,G两点,与三角形ABC两边相交于E,D两点.设弧 ![]() 的长为x(0<x<π),y=EB+BC+CD,若l从l1平行移动到l2 , 则函数y=f(x)的图象大致是( )
的长为x(0<x<π),y=EB+BC+CD,若l从l1平行移动到l2 , 则函数y=f(x)的图象大致是( ) 
A.
B.
C.
D.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)设直线l过点(2,3)且与直线2x+y+1=0垂直,l与x轴,y轴分别交于A、B两点,求|AB|;
(2)求过点A(4,-1)且在x轴和y轴上的截距相等的直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设△AnBnCn的三边长分别为an , bn , cn , △AnBnCn的面积为Sn , n=1,2,3…若b1>c1 , b1+c1=2a1 , an+1=an , ![]() ,
, ![]() ,则( )
,则( )
A.{Sn}为递减数列
B.{Sn}为递增数列
C.{S2n﹣1}为递增数列,{S2n}为递减数列
D.{S2n﹣1}为递减数列,{S2n}为递增数列
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com