
【题目】已知函数![]() ,
, ![]() .
.
(Ⅰ)若![]() ,求
,求![]() 的单调区间;
的单调区间;
(Ⅱ)若对任意的![]() ,
, ![]()
![]() 都有
都有![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)![]() 的单调递增区间是
的单调递增区间是![]() ,单调递减区间是
,单调递减区间是![]() .(Ⅱ)
.(Ⅱ) ![]()
【解析】试题分析:(1)将![]() 代入表达式,求导,研究导函数的正负,从而得到单调区间;(2)先求出
代入表达式,求导,研究导函数的正负,从而得到单调区间;(2)先求出![]() 在
在![]() 上的最大值为
上的最大值为![]() ,问题转化为
,问题转化为![]() 恒成立,变量分离得到
恒成立,变量分离得到![]() 对任意的
对任意的![]() 恒成立,转化为求函数
恒成立,转化为求函数![]() 的最值。
的最值。
解析:
(Ⅰ)若![]() ,则
,则![]()
![]() ,
, ![]() ,
,
由![]() 得
得![]() ;由
;由![]() 得
得![]() ,
,
所以![]() 的单调递增区间是
的单调递增区间是![]() ,单调递减区间是
,单调递减区间是![]() .
.
(Ⅱ)![]() ,所以当
,所以当![]() 时,
时, ![]() ,
, ![]() 单调递减;
单调递减;
当![]() 时,
时, ![]() ,
, ![]() 单调递增,
单调递增,
又![]() ,
, ![]() ,所以
,所以![]() 在
在![]() 上的最大值为
上的最大值为![]() .
.
由题意,若对任意的![]() ,都有
,都有![]() 成立,
成立,
即对任意的![]() ,都有
,都有![]() 恒成立,即
恒成立,即![]() 恒成立,
恒成立,
即![]() 对任意的
对任意的![]() 恒成立,所以
恒成立,所以![]() .
.
设![]() ,
, ![]() ,则
,则![]() ,
, ![]() ,
,
所以![]() 在
在![]() 上单调递减,则
上单调递减,则![]() ,
,
所以![]() 在
在![]() 上单调递减,又
上单调递减,又![]() ,
,
所以当![]() 时,
时, ![]() ,
, ![]() 单调递增;
单调递增;
当![]() 时,
时, ![]() ,
, ![]() 单调递减,
单调递减,
∴![]() 在
在![]() 上的最大值为
上的最大值为![]() ,∴
,∴![]() ,
,
所以![]() 的取值范围是
的取值范围是![]() .
.
点睛:这个题目考查了导数在研究函数的单调性中的应用,在研究函数最值的应用;对于函数恒成立或者有解求参的问题,常用方法有:变量分离,参变分离,转化为函数最值问题;或者直接求函数最值,使得函数最值大于或者小于0;或者分离成两个函数,使得一个函数恒大于或小于另一个函数。


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】衡阳市为增强市民的环境保护意识,面向全市征召义务宣传志愿者,现从符合条件的志愿者中随机抽取100名后按年龄分组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.
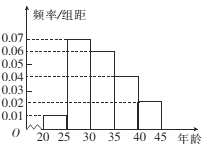
(1)若从第3,4,5组中用分层抽样的方法抽取6名志愿者参加广场的宣传活动,则应从第3,4,5组各抽取多少名志愿者?
(2)在(1)的条件下,该市决定在第3,4组的志愿者中随机抽取2名志愿者介绍宣传经验,求第4组至少有一名志愿者被抽中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2017·黄冈质检)设等比数列{an}的各项均为正数,公比为q,前n项和为Sn.若对任意的n∈N*,有S2n<3Sn,则q的取值范围是( )
A. (0,1] B. (0,2)
C. [1,2) D. (0, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为了准确把握市场,做好产品计划,特对某产品做了市场调查:先销售该产品50天,统计发现每天的销售量![]() 分布在
分布在![]() 内,且销售量
内,且销售量![]() 的分布频率
的分布频率
 .
.
(Ⅰ)求![]() 的值.
的值.
(Ⅱ)若销售量大于等于80,则称该日畅销,其余为滞销,根据是否畅销从这50天中用分层抽样的方法随机抽取5天,再从这5天中随机抽取2天,求这2天中恰有1天是畅销日的概率(将频率视为概率).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com