
 | 赞成 | 反对 | 无所谓 |
| 农村居民 | 2100人 | 120人 | y人 |
| 城镇居民 | 600人 | x人 | z人 |
 的分布列和数学期望.
的分布列和数学期望. =0.05,解得x=60.
=0.05,解得x=60. =72人.
=72人.  =4人,城镇居民为
=4人,城镇居民为 =2人,
=2人, ,P(ξ=2)=
,P(ξ=2)= ,P(ξ=3)=
,P(ξ=3)= ,
,| ξ | 1 | 2 | 3 |
| P |  |  |  |
 +2×
+2× +3×
+3× =2.
=2. 

科目:高中数学 来源:不详 题型:解答题
 ,且相互间没有影响.
,且相互间没有影响. ,试求
,试求 的分布列和数学期望.
的分布列和数学期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 品种甲 | 403 | 397 | 390 | 404 | 388 | 400 | 412 | 406 |
| 品种乙 | 419 | 403 | 412 | 418 | 408 | 423 | 400 | 413 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 ,P(X=x2)=
,P(X=x2)= ,且x1<x2,又已知E(X)=
,且x1<x2,又已知E(X)= ,V(X)=
,V(X)= ,则x1+x2的值为________.
,则x1+x2的值为________.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
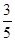 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,服用B有效的概率为
,服用B有效的概率为 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com