
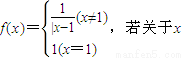 的方程
的方程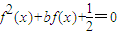 有5个不同的根x1、x2、x3、x4、x5,则x12+x22+x32+x42+x52等于 .
有5个不同的根x1、x2、x3、x4、x5,则x12+x22+x32+x42+x52等于 . 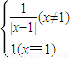 的表达式可对x分x=1与x≠1讨论,由方程
的表达式可对x分x=1与x≠1讨论,由方程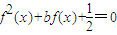 分别求得x1、x2、x3、x4、x5,从而可求得则x12+x22+x32+x42+x52的值.
分别求得x1、x2、x3、x4、x5,从而可求得则x12+x22+x32+x42+x52的值. =0,b=-
=0,b=- ;
;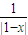 ,方程
,方程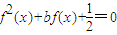 可化为:
可化为: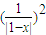 -
- •
•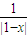 +
+ =0,
=0,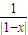 -1)•(2•
-1)•(2•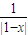 -1)=0,
-1)=0,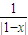 =1或
=1或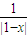 =
= ,
,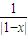 =1得:x=0或x=2;解
=1得:x=0或x=2;解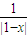 =
= 得:x=-1或x=3;
得:x=-1或x=3;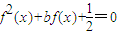 分别求得x1、x2、x3、x4、x5,
分别求得x1、x2、x3、x4、x5, 

 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:高中数学 来源: 题型:
| 1 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分12分)
一个盒子装有六张卡片,上面分别写着如下六个定义域为R的函数:
![]()
(1)现从盒子中任取两张卡片,将卡片上的函数相加得一个新函数,求所得函数是偶函数的概率;
(2)现从盒子中进行逐一抽取卡片,且每次取出后均不放回,若取到一张记有奇函数的卡片则停止抽取,否则继续进行. 求抽取次数![]() 的分布列、数学期望和方差.
的分布列、数学期望和方差.
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 1 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com