
如图,已知DE⊥平面ACD,DE//AB,△ACD是正三角形,AD=DE=2AB,且F是CD的中点。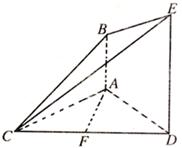
(I)求证:AF//平面BCE;
(II)求证:平面BCE⊥平面CDE;
(III)求平面BCE与平面ACD所成锐二面角的大小。
(I)(II)见试题解析;(III) .
.
解析试题分析:(I)要证明线面垂直,就是要在平面BCE中找一条与AF垂直的直线,这条直线容易看出是平面BAF与平面BCE的交线,当然根据已知条件,辅助线可直接取CE中点P,直线BP就是我们要找的平等线;(II)本证面面垂直,先要证线面垂直,先看题中有没有已知的垂直关系,发现有直线AF与平面CDE垂直,而在(I)的证明中有BP//AF,BP就是我们要找的线面垂直中的线;(III)平面BCE与平面ACD有一个公共点C,依据二面角的定义,要选作出二面角的棱,然后作出平面角,才能求出二面角的大小,但由(I)题中有两两垂直的三条直线FA,FP,AD,故我们可建立空间直角坐标系,通过空间向量来求二面角大小.
试题解析:(I)解:取CE中点P,连结FP、BP,∵F为CD的中点,
∴FP//DE,且FP= 又AB//DE,且AB=
又AB//DE,且AB=
∴AB//FP,且AB=FP, ∴ABPF为平行四边形,∴AF//BP。
又∵AF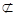 平面BCE,BP
平面BCE,BP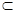 平面BCE, ∴AF//平面BCE。 3分
平面BCE, ∴AF//平面BCE。 3分
(II)∵△ACD为正三角形,∴AF⊥CD。∵AB⊥平面ACD,DE//AB,
∴DE⊥平面ACD,又AF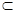 平面ACD,∴DE⊥AF。又AF⊥CD,CD∩DE=D,
平面ACD,∴DE⊥AF。又AF⊥CD,CD∩DE=D,
∴AF⊥平面CDE。又BP//AF,∴BP⊥平面CDE。
又∵BP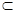 平面BCE,∴平面BCE⊥平面CDE。 7分
平面BCE,∴平面BCE⊥平面CDE。 7分
(III)由(II),以F为坐标原点,FA,FD,FP所在的直线分别为x,y,z轴(如图),建立空间直角坐标系F—xyz.设AC=2,则C(0,—1,0),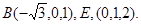

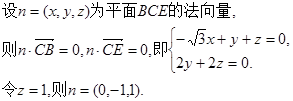
显然, 为平面ACD的法向量。
为平面ACD的法向量。
设平面BCE与平面ACD所成锐二面角为
 ,
,
即平面BCE与平面ACD所成锐二面角为45°。 13分
考点:(I)线面平行;(II)面面垂直;(III)二面角.


科目:高中数学 来源: 题型:填空题
已知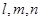 是三条不同的直线,
是三条不同的直线,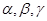 是三个不同的平面,下列命题:
是三个不同的平面,下列命题:
①若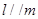 ,
,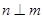 ,则
,则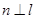 ; ②若
; ②若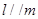 ,
,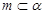 ,则
,则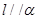 ;
;
③若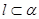 ,
,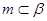 ,
,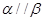 ,则
,则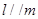 ; ④若
; ④若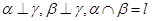 ,则
,则 .
.
其中真命题是_ __.(写出所有真命题的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
如图,直三棱柱ABCA1B1C1中,AB=AC=1,AA1=2,∠B1A1C1=90°,D为BB1的中点,则异面直线C1D与A1C所成角的余弦值为__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com