
【题目】已知函数f(x)=tx,(x∈R).
(1)若t=ax+b,a,b∈R,且﹣1≤f(﹣1)≤2,2≤f(1)≤4,求点(a,b)的集合表示的平面区域的面积;
(2)若t=2+ ![]() ,(x<1且x≠0),求函数f(x)的最大值;
,(x<1且x≠0),求函数f(x)的最大值;
(3)若t=x﹣a﹣3(a∈R),不等式b2+c2﹣bc﹣3b﹣1≤f(x)≤a+4(b,c∈R)的解集为[﹣1,5],求b,c的值.
【答案】
(1)解:当t=ax+b时,f(x)=ax2+bx,
由﹣1≤f(﹣1)≤2,2≤f(1)≤4,
可得﹣1≤a﹣b≤2,2≤a+b≤4,
由两平行直线x﹣y=2和x﹣y=﹣1的距离为 ![]() ,
,
两平行直线x+y=2和x+y=4的距离为 ![]() ,
,
可得点(a,b)的集合表示的平面区域(矩形)的面积为 ![]() ×
× ![]() =3
=3
(2)解:若t=2+ ![]() ,(x<1且x≠0),
,(x<1且x≠0),
则f(x)=2x+ ![]() (x<1且x≠0),
(x<1且x≠0),
由2x+ ![]() =[2(x﹣1)+
=[2(x﹣1)+ ![]() ]+2=﹣[2(1﹣x)+
]+2=﹣[2(1﹣x)+ ![]() ]+2
]+2
≤﹣2 ![]() +2=2﹣2
+2=2﹣2 ![]() ,
,
当且仅当2(1﹣x)= ![]() ,即x=1﹣
,即x=1﹣ ![]() 时,等号成立,
时,等号成立,
则函数的最大值为2﹣2 ![]()
(3)解:若t=x﹣a﹣3(a∈R),则f(x)=x2﹣(a+3)x,
f(x)≤a+4(b,c∈R)的解集为[﹣1,5],
即x2﹣(a+3)x﹣(a+4)≤0的解集为[﹣1,5],
即﹣1,5为方程x2﹣(a+3)x﹣(a+4)=0的两根,
可得﹣1+5=a+3,﹣1×5=﹣(a+4),
解得a=1;
再由不等式b2+c2﹣bc﹣3b﹣1≤f(x)≤a+4(b,c∈R)的解集为[﹣1,5],
可得b2+c2﹣bc﹣3b﹣1≤f(x)的最小值,
而f(x)=x2﹣4x=(x﹣2)2﹣4的最小值为﹣4,
则b2+c2﹣bc﹣3b﹣1≤﹣4,
即b2+c2﹣bc﹣3b+3≤0,
记g(c)=c2﹣bc+b2﹣3b+3,
则△=b2﹣4(b2﹣3b+3)≥0,
即﹣3(b﹣2)2≥0,但﹣3(b﹣2)2≤0,
则b=2;
即有4+c2﹣2c﹣6+3≤0,
即c2﹣2c+1≤0,即(c﹣1)2≤0,
但(c﹣1)2≥0,
即c=1
【解析】(1)由题意可得﹣1≤a﹣b≤2,2≤a+b≤4,运用点(a,b)的集合表示的平面区域为矩形,由平行直线间的距离公式,即可得到所求面积;(2)运用基本不等式,注意满足的条件:一正二定三等,即可得到所求最大值;(3)运用二次不等式的解集,可得对应方程的解,运用韦达定理可得a=1,再由不等式b2+c2﹣bc﹣3b﹣1≤f(x)的最小值,结合判别式非负,可得b=2,进而得到c的不等式,求得c=1.
【考点精析】关于本题考查的函数的最值及其几何意义,需要了解利用二次函数的性质(配方法)求函数的最大(小)值;利用图象求函数的最大(小)值;利用函数单调性的判断函数的最大(小)值才能得出正确答案.


科目:高中数学 来源: 题型:
【题目】已知数集A={a1 , a2…an}(0≤a1<a2…<an , n≥2)具有性质P;对任意的 i,j(1≤i≤j≤n),ai+aj与aj﹣ai两数中至少有一个属于A.
(1)分别判断数集{0,1,3,4}与{0,2,3,6}是否具有性质P,并说明理由;
(2)证明:a1=0,且nan=2(a1+a2+a+..+an)
(3)当n=5时若 a2=2,求集合A.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)是定义在(0,+∞)上的函数,且对任意的正实数x1 , x2均有:(x1﹣x2)[f(x1)﹣f(x2)]>0,则不等式f(x)﹣f(8x﹣16)>0的解集是( )
A.(0,+∞)
B.(0,2)
C.(2,+∞)
D.(2, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】求适合下列条件的圆锥曲线的标准方程:
(1)焦点坐标为( ![]() ,0),准线方程为x=
,0),准线方程为x= ![]() 的椭圆;
的椭圆;
(2)过点( ![]() ,2),渐近线方程为y=±2x的双曲线.
,2),渐近线方程为y=±2x的双曲线.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2017江西4月质检】已知椭圆![]() 的离心率为
的离心率为![]() ,且过点
,且过点![]() .
.

(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 且斜率大于0的直线
且斜率大于0的直线![]() 与椭圆
与椭圆![]() 相交于点
相交于点![]() ,
,![]() ,直线
,直线![]() ,
,![]() 与
与![]() 轴相交于
轴相交于![]() ,
,![]() 两点,求
两点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax﹣1(a>0,且a≠1),当x∈(0,+∞)时,f(x)>0,且函数g(x)=f(x+1)﹣4的图象不过第二象限,则a的取值范围是( )
A.(1,+∞)
B.![]()
C.(1,3]
D.(1,5]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2017广东佛山二模】某保险公司针对企业职工推出一款意外险产品,每年每人只要交少量保费,发生意外后可一次性获赔50万元.保险公司把职工从事的所有岗位共分为![]() 、
、![]() 、
、![]() 三类工种,根据历史数据统计出三类工种的每赔付频率如下表(并以此估计赔付概率).
三类工种,根据历史数据统计出三类工种的每赔付频率如下表(并以此估计赔付概率).
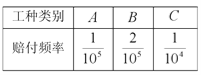
(Ⅰ)根据规定,该产品各工种保单的期望利润都不得超过保费的20%,试分别确定各类工种每张保单保费的上限;
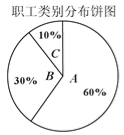
(Ⅱ)某企业共有职工20000人,从事三类工种的人数分布比例如图,老板准备为全体职工每人购买一份此种保险,并以(Ⅰ)中计算的各类保险上限购买,试估计保险公司在这宗交易中的期望利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2017福建三明5月质检】某市政府为了引导居民合理用水,决定全面实施阶梯水价,阶梯水价原则上以住宅(一套住宅为一户)的月用水量为基准定价:若用水量不超过12吨时,按4元/吨计算水费;若用水量超过12吨且不超过14吨时,超过12吨部分按6.60元/吨计算水费;若用水量超过14吨时,超过14吨部分按7.80元/吨计算水费.为了了解全市居民月用水量的分布情况,通过抽样,获得了100户居民的月用水量(单位:吨),将数据按照![]() 分成8组,制成了如图1所示的频率分布直方图.
分成8组,制成了如图1所示的频率分布直方图.

(Ⅰ)假设用抽到的100户居民月用水量作为样本估计全市的居民用水情况.
(ⅰ)现从全市居民中依次随机抽取5户,求这5户居民恰好3户居民的月用水用量都超过12吨的概率;
(ⅱ)试估计全市居民用水价格的期望(精确到0.01);
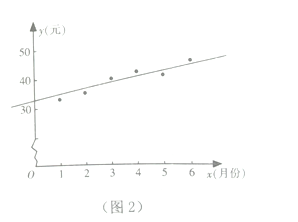
(Ⅱ)如图2是该市居民李某2016年1~6月份的月用水费![]() (元)与月份
(元)与月份![]() 的散点图,其拟合的线性回归方程是
的散点图,其拟合的线性回归方程是![]() .若李某2016年1~7月份水费总支出为294.6元,试估计李某7月份的用水吨数.
.若李某2016年1~7月份水费总支出为294.6元,试估计李某7月份的用水吨数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,AB=1,AC=AA1=![]() , ∠ABC=60°.
, ∠ABC=60°.
(1)证明:AB⊥A1C;
(2)求二面角A﹣A1C﹣B的大小.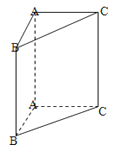
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com