练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知椭圆长轴长|A1A2|=6，焦距|F1F2|=4，过椭圆焦点F1作一直线时，交椭圆于两点M、N，设MN的倾斜角为α，当α取什么值时，|MN|等于椭圆短轴长？

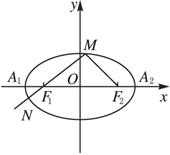
    解：如图所示,以椭圆的长轴A1A2所在直线为x轴,椭圆中心为原点建立直角坐标系,依题意2a=6,a=3,2c=4,c=2.

    ∴b==1,∴椭圆方程为+y2=1,e==.

    设M（x1,y1）,N（x2,y2）,由椭圆的焦半径公式知:

    ｜MF1｜=a+ex1=3+x1,｜NF1｜=a+ex2=3+x2.?

    ∴｜MN｜=｜MF1｜+｜NF1｜=6+（x1+x2）.?

    又直线MN的方程为y=（x+2）tan α（α≠）,将其代入椭圆方程,整理,得:

    （1+9tan2α）x2+36xtan2α+72tan2α-9=0.?

    ∴x1+x2=.又｜MN｜=2,

    ∴6+（x1+x2）=2,?

    ∴6＋（）=2,?

    解得tan2α=,?

    ∴tanα=±.?

    ∵0≤α＜π且α≠,?

    ∴α=或π,即当α=或α=时,｜MN｜等于椭圆的短轴长.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知椭圆C的离心率e=
    		3
    2
    ，长轴的左右端点分别为A1（-2，0），A2（2，0）．
    （Ⅰ）求椭圆C的方程；
    （Ⅱ）设直线x=my+1与椭圆C交于P，Q两点，直线A1P与A2Q交于点S，试问：当m变化时，点S是否恒在一条定直线上？若是，请写出这条直线方程，并证明你的结论；若不是，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知椭圆C：
    x2
    a2
    +
    y2
    b2
    =1（a＞b＞0）的离心率e=
    		3
    2
    ，椭圆C的上、下顶点分别为A1，A2，左、右顶点分别为B1，B2，左、右焦点分别为F1，F2．原点到直线A2B2的距离为
    2
    		5
    5
    ．
    （1）求椭圆C的方程；
    （2）过原点且斜率为
    1
    2
    的直线l，与椭圆交于E，F点，试判断∠EF2F是锐角、直角还是钝角，并写出理由；
    （3）P是椭圆上异于A1，A2的任一点，直线PA1，PA2，分别交x轴于点N，M，若直线OT与过点M，N的圆G相切，切点为T．证明：线段OT的长为定值，并求出该定值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2011•浦东新区三模）已知椭圆C的长轴长是焦距的两倍，其左、右焦点依次为F1、F2，抛物线M：y2=4mx（m＞0）的准线与x轴交于F1，椭圆C与抛物线M的一个交点为P．
    （1）当m=1时，求椭圆C的方程；
    （2）在（1）的条件下，直线l过焦点F2，与抛物线M交于A、B两点，若弦长|AB|等于△PF1F2的周长，求直线l的方程；
    （3）由抛物线弧y2=4mx(0≤x≤
    2m
    3
    )    和椭圆弧
    x2
    4m2
    +
    y2
    3m2
    =1    (
    2m
    3
    ≤x≤2m)
    （m＞0）合成的曲线叫“抛椭圆”，是否存在以原点O为直角顶点，另两个顶点A1、A2落在“抛椭圆”上的等腰直角三角形OA1A2，若存在，求出两直角边所在直线的斜率；若不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2012•江门一模）已知椭圆C的中心在原点，长轴在x轴上，经过点A（0，1），离心率e=
    		2
    2
    ．
    （1）求椭圆C的方程；
    （2）设直线ln：y=
    1
    n+1
    （n∈N*）与椭圆C在第一象限内相交于点An（xn，yn），记an=
    1
    2
    x
     
    2
    n
    ，试证明：对?n∈N*，a1•a2•…•an＞
    1
    2
    ．

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年天津市高三第四次月考文科数学试卷（解析版） 题型：解答题

    已知椭圆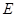: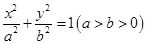的一个焦点为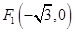且过点.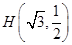

    （Ⅰ）求椭圆E的方程；

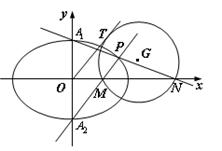
    （Ⅱ）设椭圆E的上下顶点分别为A1，A2，P是椭圆上异于A1，A2的任一点，直线PA1，PA2分别交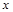轴于点N，M，若直线OT与过点M，N的圆G相切，切点为T．

    证明：线段OT的长为定值，并求出该定值．

     

    查看答案和解析>>

    同步练习册答案