
已知偶函数 满足:当
满足:当 时,
时, ,当
,当 时,
时, .
.
(Ⅰ).求 表达式;
表达式;
(Ⅱ).若直线 与函数
与函数 的图像恰有两个公共点,求实数
的图像恰有两个公共点,求实数 的取值范围;
的取值范围;
(Ⅲ).试讨论当实数 满足什么条件时,直线
满足什么条件时,直线 的图像恰有
的图像恰有 个公共点
个公共点 ,且这
,且这 个公共点均匀分布在直线
个公共点均匀分布在直线 上.(不要求过程)
上.(不要求过程)
(Ⅰ).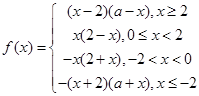 ;(Ⅱ).
;(Ⅱ).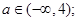 (Ⅲ).当
(Ⅲ).当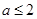 时,
时,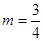 或
或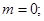
当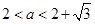 时,
时,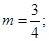 此时
此时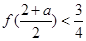 ; 当
; 当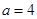 时,
时,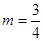 ,
, 或
或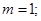
当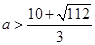 时
时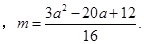 此时
此时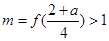 .
.
解析试题分析:(1)由 为偶函数,则有
为偶函数,则有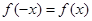 ,又因为当
,又因为当 ,
,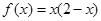 及
及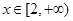 ,
, ,所以当
,所以当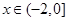 时,
时,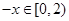 ,
,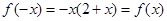 即可求出
即可求出 .当
.当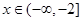 时,
时,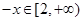 同理可求出此时的
同理可求出此时的 .(2)画出
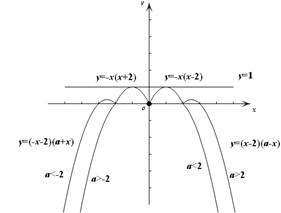
.(2)画出 的大致图像,由图1易知,当
的大致图像,由图1易知,当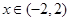 时,函数
时,函数 与
与 恰有两个交点,所以当
恰有两个交点,所以当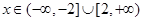 时,函数
时,函数 与
与 无交点,易得当
无交点,易得当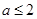 时恒成立,当
时恒成立,当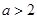 时,则有
时,则有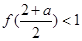 ,即可求出
,即可求出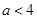 .
.
当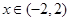 ,
,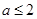 时,函数
时,函数 的图像如图2所示,此时直线
的图像如图2所示,此时直线 的图像若恰有
的图像若恰有 个公共点
个公共点 ,且这
,且这 个公共点均匀分布在直线
个公共点均匀分布在直线 上,则易知
上,则易知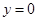 时符合题意,设
时符合题意,设 时由左到右的两个交点的横坐标分别为
时由左到右的两个交点的横坐标分别为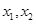 ,由函数的对称性易知,
,由函数的对称性易知,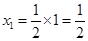 ,此时
,此时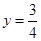 .其他情况同理即可求出.
.其他情况同理即可求出.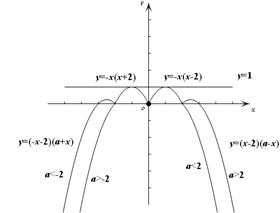
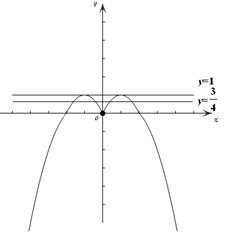
图1 图2
试题解析:(1)
 为偶函数,则有
为偶函数,则有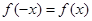
当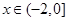 时,
时,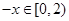 ,
,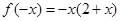 即
即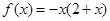
当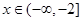 时,
时,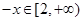 ,
,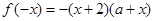 即
即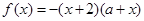
故有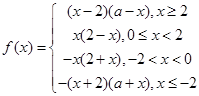
(2)如下图,当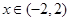 时,由图像易知函数
时,由图像易知函数 与
与 恰有两个交点
恰有两个交点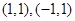
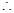 当
当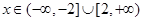 时,函数
时,函数 与
与 无交点
无交点
由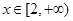 ,
,
当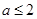 时,此时符合题意
时,此时符合题意
当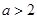 时,由
时,由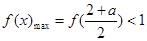 即
即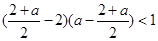
可得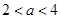
由偶函数的对称性可知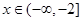 时,
时,
与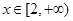 时的情况相同
时的情况相同
故综上: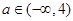
(3)当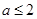


 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:高中数学 来源: 题型:解答题
某地开发了一个旅游景点,第1年的游客约为100万人,第2年的游客约为120万人.某数学兴趣小组综合各种因素预测:①该景点每年的游客人数会逐年增加;②该景点每年的游客都达不到130万人.该兴趣小组想找一个函数 来拟合该景点对外开放的第
来拟合该景点对外开放的第
 年与当年的游客人数
年与当年的游客人数 (单位:万人)之间的关系.
(单位:万人)之间的关系.
(1)根据上述两点预测,请用数学语言描述函数 所具有的性质;
所具有的性质;
(2)若 =
= ,试确定
,试确定 的值,并考察该函数是否符合上述两点预测;
的值,并考察该函数是否符合上述两点预测;
(3)若 =
= ,欲使得该函数符合上述两点预测,试确定
,欲使得该函数符合上述两点预测,试确定 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com