
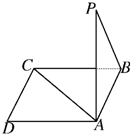
 如图所示,点P在正方形ABCD所在平面外,PA⊥平面ABCD,PA=AB,则PB与AC所成的角是
如图所示,点P在正方形ABCD所在平面外,PA⊥平面ABCD,PA=AB,则PB与AC所成的角是 科学实验活动册系列答案
科学实验活动册系列答案科目:高中数学 来源:福建省四地六校2012届高三上学期第三次月考数学理科试题 题型:013
定义:平面内两条相交但不垂直的数轴构成的坐标系(两条数轴的原点重合且单位长度相同)称为平面斜坐标系;在平面斜坐标系xOy中,若 (其中
(其中 分别是斜坐标系x轴、y轴正方向上的单位向量,x、y∈R,O为坐标原点),则有序实数对(x,y)称为点P的斜坐标.如图所示,在平面斜坐标系xOy中,若∠xOy=120°,点A(1,0),P为单位圆上一点,且∠AOP=
分别是斜坐标系x轴、y轴正方向上的单位向量,x、y∈R,O为坐标原点),则有序实数对(x,y)称为点P的斜坐标.如图所示,在平面斜坐标系xOy中,若∠xOy=120°,点A(1,0),P为单位圆上一点,且∠AOP=![]() ,点P在平面斜坐标系中的坐标是
,点P在平面斜坐标系中的坐标是



(sin![]() ,cos
,cos![]() )
)
(cos![]() ,sin
,sin![]() )
)
查看答案和解析>>
科目:高中数学 来源:同步题 题型:解答题
 的概率P1;
的概率P1; 的概率P2。
的概率P2。
查看答案和解析>>
科目:高中数学 来源:福建省月考题 题型:单选题
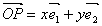 (其中
(其中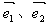 分别是斜坐标系x轴、y轴正方向上的单位向量,x、y∈R,O为坐标原点),则有序实数对(x,y)称为点P的斜坐标。如图所示,在平面斜坐标系xOy中,若∠xOy=120°,点A(1,0),P为单位圆上一点,且∠AOP=θ,点P在平面斜坐标系中的坐标是
分别是斜坐标系x轴、y轴正方向上的单位向量,x、y∈R,O为坐标原点),则有序实数对(x,y)称为点P的斜坐标。如图所示,在平面斜坐标系xOy中,若∠xOy=120°,点A(1,0),P为单位圆上一点,且∠AOP=θ,点P在平面斜坐标系中的坐标是
[ ]
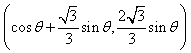
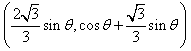
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com