
小波以游戏方式决定:是去打球、唱歌还是去下棋.游戏规则为:以O为起点,再从A1,A2,A3,A4,A5,A6(如图)这6个点中任取两点分别为终点得到两个向量,记这两个向量的数量积为X,若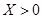 就去打球;若
就去打球;若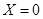 就去唱歌;若
就去唱歌;若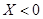 就去下棋.
就去下棋.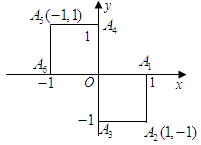
(Ⅰ) 写出数量积X的所有可能取值;
(Ⅱ)分别求小波去下棋的概率和不去唱歌的概率.
(Ⅰ) 的所有可能取值为
的所有可能取值为 ;(Ⅱ)小波去下棋的概率为
;(Ⅱ)小波去下棋的概率为 ,小波不去唱歌的概率
,小波不去唱歌的概率 .
.
解析试题分析:(Ⅰ)
科目:高中数学
来源:
题型:解答题
淮南八公山某种豆腐食品是经过A、B、C三道工序加工而成的,A、B、C工序的产品合格率分别为
科目:高中数学
来源:
题型:解答题
现有甲、乙两个靶.某射手向甲靶射击两次,每次命中的概率为
科目:高中数学
来源:
题型:解答题
我校社团联即将举行一届象棋比赛,规则如下:两名选手比赛时,每局胜者得
科目:高中数学
来源:
题型:解答题
在一次数学考试中,第22,23,24题为选做题,规定每位考生必须且只须在其中选做一题,设5名考生选做这三题的任意一题的可能性均为
科目:高中数学
来源:
题型:解答题
在甲、乙两个盒子中分别装有标号为1、2、3、4的四个球,现从甲、乙两个盒子中各取出1个球,每个小球被取出的可能性相等.
科目:高中数学
来源:
题型:解答题
某经销商试销A、B两种商品一个月(30天)的记录如下:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区 的所有可能取值,即从
的所有可能取值,即从 ,
, ,
, ,
, ,
, ,
, 这六个向量中任取两个,共有
这六个向量中任取两个,共有 种,而对取出两个向量的数量积进行计算,得到
种,而对取出两个向量的数量积进行计算,得到 的所有可能取值为
的所有可能取值为 ;(Ⅱ)求小波去下棋的概率,这显然是古典概型,只需找出总的事件数有
;(Ⅱ)求小波去下棋的概率,这显然是古典概型,只需找出总的事件数有 种,因为
种,因为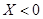 就去下棋,只需在(Ⅰ)计算中,找出小于零的次数为
就去下棋,只需在(Ⅰ)计算中,找出小于零的次数为 ,有古典概型的概率求法知:小波去下棋的概率为
,有古典概型的概率求法知:小波去下棋的概率为 ,小波不去唱歌的概率,它的对立事件为,去唱歌,而
,小波不去唱歌的概率,它的对立事件为,去唱歌,而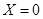 就去唱歌,在(Ⅰ)计算中,
就去唱歌,在(Ⅰ)计算中,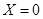 共有四次,故去唱歌的概率为
共有四次,故去唱歌的概率为 ,有对立事件的概率求法知:小波不去唱歌的概率
,有对立事件的概率求法知:小波不去唱歌的概率 .
.
试题解析:(Ⅰ)由上表可知 的所有可能取值为
的所有可能取值为 ;
;







1 0 0 -1 -1 
1 -1 -2 -1<


创优考100分系列答案
高分中考系列答案

中考专项突破系列答案
全能金卷小学毕业升学全程总复习系列答案
新课程同步导学练测八年级英语下册系列答案
精致课堂有效反馈系列答案
小考状元必备测试卷系列答案
全能小考王小升初名校备考密卷系列答案
中考5月冲关卷系列答案
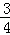 、
、 、
、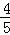 .已知每道工序的加工都相互独立,三道工序加工的产品都为合格时产品为一等品;有两次合格为二等品;其它的为废品,不进入市场.
.已知每道工序的加工都相互独立,三道工序加工的产品都为合格时产品为一等品;有两次合格为二等品;其它的为废品,不进入市场.
(Ⅰ)正式生产前先试生产2袋食品,求这2袋食品都为废品的概率;
(Ⅱ)设ξ为加工工序中产品合格的次数,求ξ的分布列和数学期望.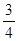 ,每命中一次得1分,没有命中得0分;向乙靶射击一次,命中的概率为
,每命中一次得1分,没有命中得0分;向乙靶射击一次,命中的概率为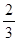 ,命中得2分,没有命中得0分.该射手每次射击的结果相互独立.假设该射手完成以上三次射击.
,命中得2分,没有命中得0分.该射手每次射击的结果相互独立.假设该射手完成以上三次射击.
(I)求该射手恰好命中两次的概率;
(II)求该射手的总得分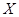 的分布列及数学期望
的分布列及数学期望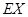 ;
;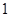 分,负者得
分,负者得 分,比赛进行到有一人比对方多
分,比赛进行到有一人比对方多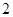 分或打满
分或打满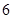 局时结束.假设选手甲与选手乙比赛时,甲每局获胜的概率皆为
局时结束.假设选手甲与选手乙比赛时,甲每局获胜的概率皆为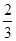 ,且各局比赛胜负互不影响.
,且各局比赛胜负互不影响.
(Ⅰ)求比赛进行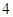 局结束,且乙比甲多得
局结束,且乙比甲多得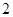 分的概率;
分的概率;
(Ⅱ)设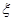 表示比赛停止时已比赛的局数,求随机变量
表示比赛停止时已比赛的局数,求随机变量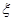 的分布列和数学期望.
的分布列和数学期望.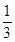 ,每位学生对每题的选择是相互独立的,各学生的选择相互之间没有影响.
,每位学生对每题的选择是相互独立的,各学生的选择相互之间没有影响.
(1)求其中甲、乙两人选做同一题的概率;
(2)设选做第23题的人数为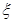 ,求
,求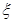 的分布列及数学期望.
的分布列及数学期望.
(1)求取出的两个球上标号为相邻整数的概率;
(2)求取出的两个球上标号之和能被3整除的概率
若售出每种商品1件均获利40元,用日销售量(件) 0 1 2 3 4 5 商品A的频数 3 5 7 7 5 3 商品B的频数 4 4 6 8 5 3 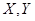 表示售出A、B商品的日利润值(单位:元).将频率视为概率.
表示售出A、B商品的日利润值(单位:元).将频率视为概率.
(Ⅰ)设两种商品的销售量互不影响,求两种商品日获利值均超过100元的概率;
(Ⅱ)由于某种原因,该商家决定只选择经销A、B商品的一种,你认为应选择哪种商品,说明理由.
版权声明:本站所有文章,图片来源于网络,著作权及版权归原作者所有,转载无意侵犯版权,如有侵权,请作者速来函告知,我们将尽快处理,联系qq:3310059649。
ICP备案序号: 沪ICP备07509807号-10 鄂公网安备42018502000812号