
【题目】如图,半径为![]() 的圆形纸板内有一个相同圆心的半径为
的圆形纸板内有一个相同圆心的半径为![]() 的小圆,现将半径为
的小圆,现将半径为![]() 的一枚硬币抛到此纸板上,使整块硬币完全随机落在纸板内,则硬币与小圆无公共点的概率为( )
的一枚硬币抛到此纸板上,使整块硬币完全随机落在纸板内,则硬币与小圆无公共点的概率为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】由题意可得,硬币要落在纸板内,硬币圆心距离纸板圆心的距离应该小于4.硬币与小圆无公共点,硬币圆心距离小圆圆心要大于2,先求出硬币落在纸板上的面积,然后再求解硬币落下后与小圆没交点的区域的面积,代入古典概率的计算公式可求
解答:解:记“硬币落下后与小圆无公共点”为事件A
硬币要落在纸板内,硬币圆心距离纸板圆心的距离应该小于4,其面积为16π
无公共点也就意味着,硬币的圆心与纸板的圆心相距超过2cm
以纸板的圆心为圆心,作一个半径2cm的圆,硬币的圆心在此圆外面,则硬币与半径为1cm的小圆无公共点
所以有公共点的概率为4/16
无公共点的概率为P(A)=1-4/16=3/4
故答案为D


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:高中数学 来源: 题型:
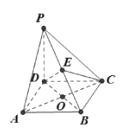
【题目】如图,在四棱锥![]() 中,
中, ![]() 平面
平面![]() ,四边形
,四边形![]() 是菱形,
是菱形, ![]() ,
, ![]() ,且
,且![]() ,
, ![]() 交于点
交于点![]() ,
, ![]() 是
是![]() 上任意一点.
上任意一点.
(1)求证: ![]() ;
;
(2)已知二面角![]() 的余弦值为
的余弦值为![]() ,若
,若![]() 为
为![]() 的中点,求
的中点,求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校艺术节对同一类的![]() ,
, ![]() ,
, ![]() ,
, ![]() 四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品获奖情况预测如下:
四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品获奖情况预测如下:
甲说:“![]() 或
或![]() 作品获得一等奖”
作品获得一等奖”
乙说:“![]() 作品获得一等奖”
作品获得一等奖”
丙说:“![]() ,
, ![]() 两项作品未获得一等奖”
两项作品未获得一等奖”
丁说:“![]() 作品获得一等奖”.
作品获得一等奖”.
若这四位同学中只有两位说的话是对的,则获得一等奖的作品是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂生产一种仪器的元件,由于受生产能力和技术水平的限制,会产生一些次品,根据经验知道,其次品率P与日产量x(万件)之间大体满足关系: 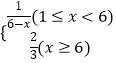 .(注:次品率=次品数/生产量,如P=0.1表示每生产10件产品,有1件为次品,其余为合格品).已知每生产1万件合格的元件可以盈利2万元,但每生产1万件次品将亏损1万元,故厂方希望定出合适的日产量.
.(注:次品率=次品数/生产量,如P=0.1表示每生产10件产品,有1件为次品,其余为合格品).已知每生产1万件合格的元件可以盈利2万元,但每生产1万件次品将亏损1万元,故厂方希望定出合适的日产量.
(1)试将生产这种仪器的元件每天的盈利额T(万元)表示为日产量x(万件)的函数;
(2)当日产量x为多少时,可获得最大利润?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=Asin(ωx+φ)(A>0,|φ|< ![]() )其中的图象如图所示,为了得到g(x)=cos(2x﹣
)其中的图象如图所示,为了得到g(x)=cos(2x﹣ ![]() )的图象,只需将f(x)的图象( )
)的图象,只需将f(x)的图象( ) 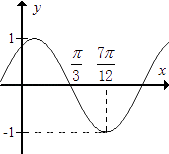
A.向左平移 ![]() 个单位
个单位
B.向右平移 ![]() 个单位
个单位
C.向左平移 ![]() 个单位
个单位
D.向右平移 ![]() 个单位
个单位
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国内某知名连锁店分店开张营业期间,在固定的时间段内消费达到一定标准的顾客可进行一次抽奖活动,随着抽奖活动的有效开展,参与抽奖活动的人数越来越多,该分店经理对开业前![]() 天参加抽奖活动的人数进行统计,
天参加抽奖活动的人数进行统计, ![]() 表示开业第
表示开业第![]() 天参加抽奖活动的人数,得到统计表格如下:
天参加抽奖活动的人数,得到统计表格如下:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
经过进一步统计分析,发现![]() 与
与![]() 具有线性相关关系.
具有线性相关关系.
(1)若从这![]() 天中随机抽取两天,求至少有
天中随机抽取两天,求至少有![]() 天参加抽奖人数超过
天参加抽奖人数超过![]() 的概率;
的概率;
(2)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并估计若该活动持续
,并估计若该活动持续![]() 天,共有多少名顾客参加抽奖.
天,共有多少名顾客参加抽奖.
参考公式: 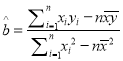 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,点
,点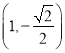 是椭圆
是椭圆![]() 上的点,离心率
上的点,离心率![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)点![]() 在椭圆
在椭圆![]() 上,若点
上,若点![]() 与点
与点![]() 关于原点对称,连接
关于原点对称,连接![]() 并延长与椭圆
并延长与椭圆![]() 的另一个交点为
的另一个交点为![]() ,连接
,连接![]() ,求
,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com