
【题目】已知0<a<b,且a+b=1,则下列不等式中正确的是( )
A.log2a>0
B.2a﹣b< ![]()
C.log2a+log2b<﹣2
D.2( ![]() +
+ ![]() )<
)< ![]()
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:高中数学 来源: 题型:
【题目】执行两次如图所示的程序框图,若第一次输入的x值为7,第二次输入的x值为9,则第一次,第二次输出的a值分别为( )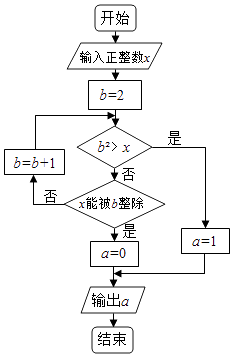
A.0,0
B.1,1
C.0,1
D.1,0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(12分)为考察某种药物预防疾病的效果,进行动物试验,调查了105个样本,统计结果为:服药的共有55个样本,服药但患病的仍有10个样本,没有服药且未患病的有30个样本.
(1)根据所给样本数据完成2×2列联表中的数据;
(2)请问能有多大把握认为药物有效?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完.根据往年销售经验,每天需求量与当天最高气温(单位:℃)有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间[20,25),需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:
最高气温 | [10,15) | [15,20) | [20,25) | [25,30) | [30,35) | [35,40) |
天数 | 2 | 16 | 36 | 25 | 7 | 4 |
以最高气温位于各区间的频率代替最高气温位于该区间的概率.
(Ⅰ)求六月份这种酸奶一天的需求量X(单位:瓶)的分布列;
(Ⅱ)设六月份一天销售这种酸奶的利润为Y(单位:元),当六月份这种酸奶一天的进货量n(单位:瓶)为多少时,Y的数学期望达到最大值?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】元旦期间,某轿车销售商为了促销,给出了两种优惠方案,顾客只能选择其中的一种,方案一:每满![]() 万元,可减
万元,可减![]() 千元;方案二:金额超过
千元;方案二:金额超过![]() 万元(含
万元(含![]() 万元),可摇号三次,其规则是依次装有
万元),可摇号三次,其规则是依次装有![]() 个幸运号、
个幸运号、![]() 个吉祥号的一个摇号机,装有
个吉祥号的一个摇号机,装有![]() 个幸运号、
个幸运号、![]() 个吉祥号的二号摇号机,装有
个吉祥号的二号摇号机,装有![]() 个幸运号、
个幸运号、![]() 个吉祥号的三号摇号机各摇号一次,其优惠情况为:若摇出
个吉祥号的三号摇号机各摇号一次,其优惠情况为:若摇出![]() 个幸运号则打
个幸运号则打![]() 折,若摇出
折,若摇出![]() 个幸运号则打
个幸运号则打![]() 折;若摇出
折;若摇出![]() 个幸运号则打
个幸运号则打![]() 折;若没有摇出幸运号则不打折.
折;若没有摇出幸运号则不打折.
(1)若某型号的车正好![]() 万元,两个顾客都选中第二中方案,求至少有一名顾客比选择方案一更优惠的概率;
万元,两个顾客都选中第二中方案,求至少有一名顾客比选择方案一更优惠的概率;
(2)若你评优看中一款价格为![]() 万的便型轿车,请用所学知识帮助你朋友分析一下应选择哪种付款方案.
万的便型轿车,请用所学知识帮助你朋友分析一下应选择哪种付款方案.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)(x∈R)满足f(x)=f(2-x),且对任意的x1,x2∈(-∞,1](x1≠x2)有(x1-x2)(f(x1)-f(x2))<0.则( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对一个样本容量为100的数据分组,各组的频数如表:
区间 | [17,19) | [19,21) | [21,23) | [23,25) | [25,27) | [27,29) | [29,31) | [31,33] |
频数 | 1 | 1 | 3 | 3 | 18 | 16 | 28 | 30 |
估计小于29的数据大约占总体的( )
A. 16% B. 40% C. 42% D. 58%
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C的参数方程是 ![]() (θ为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,A、B的极坐标分别为A﹣(2,0)、B(﹣1,
(θ为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,A、B的极坐标分别为A﹣(2,0)、B(﹣1, ![]() )
)
(1)求直线AB的直角坐标方程;
(2)在曲线C上求一点M,使点M到AB的距离最大,并求出些最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R上的函数y=f(x),满足f(2)=0,函数y=f(x+1)的图象关于点(-1,0)中心对称,且对任意的负数x1,x2(x1≠x2),![]() 恒成立,则不等式f(x)<0的解集为____.
恒成立,则不等式f(x)<0的解集为____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com