
【题目】某港口O要将一件重要物品用小艇送到一艘正在航行的轮船上,在小艇出发时,轮船位于港口的O北偏西30°且与该港口相距20海里的A处,并正以30海里/小时的航行速度沿正东方向匀速行驶.假设该小艇沿直线方向以v海里/小时的航行速度匀速行驶,经过t小时与轮船相遇.
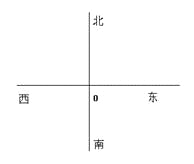
(I)若希望相遇时小艇的航行距离最小,则小艇航行速度的大小应为多少?
(II)为保证小艇在30分钟内(含30分钟)能与轮船相遇,试确定小艇航行速度的最小值.
科目:高中数学 来源: 题型:
【题目】若曲线![]() 与直线
与直线![]() 满足:①
满足:①![]() 与
与![]() 在某点
在某点![]() 处相切;②曲线
处相切;②曲线![]() 在
在![]() 附近位于直线
附近位于直线![]() 的异侧,则称曲线
的异侧,则称曲线![]() 与直线
与直线![]() “切过”.下列曲线和直线中,“切过”的有________.(填写相应的编号)
“切过”.下列曲线和直线中,“切过”的有________.(填写相应的编号)
①![]() 与
与![]() ②
②![]() 与
与![]() ③
③![]() 与
与![]()
④![]() 与
与![]() ⑤
⑤![]() 与
与![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】1,4,9,16……这些数可以用图1中的点阵表示,古希腊毕达哥拉斯学派将其称为正方形数,记第![]() 个数为
个数为![]() .在图2的杨辉三角中,第
.在图2的杨辉三角中,第![]() 行是
行是![]() 展开式的二项式系数
展开式的二项式系数![]() ,
,![]() ,…,
,…,![]() ,记杨辉三角的前
,记杨辉三角的前![]() 行所有数之和为
行所有数之和为![]() .
.

(1)求![]() 和
和![]() 的通项公式;
的通项公式;
(2)当![]() 时,比较
时,比较![]() 与
与![]() 的大小,并加以证明.
的大小,并加以证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为椭圆
为椭圆![]() 的左、右顶点,
的左、右顶点,![]() 为其右焦点,
为其右焦点,![]() 是椭圆
是椭圆![]() 上异于
上异于![]() 的动点,且
的动点,且![]() 面积的最大值为
面积的最大值为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)直线![]() 与椭圆在点
与椭圆在点![]() 处的切线交于点
处的切线交于点![]() ,当点
,当点![]() 在椭圆上运动时,求证:以
在椭圆上运动时,求证:以 ![]() 为直径的圆与直线
为直径的圆与直线![]() 恒相切.
恒相切.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知如下四个命题:①在线性回归模型中,相关指数![]() 表示解释变量
表示解释变量![]() 对于预报变量
对于预报变量![]() 的贡献率,
的贡献率,![]() 越接近于
越接近于![]() ,表示回归效果越好;②在回归直线方程
,表示回归效果越好;②在回归直线方程![]() 中,当解释变量
中,当解释变量![]() 每增加一个单位时,预报变量
每增加一个单位时,预报变量![]() 平均增加
平均增加![]() 个单位;③两个变量相关性越强,则相关系数的绝对值就越接近于
个单位;③两个变量相关性越强,则相关系数的绝对值就越接近于![]() ;④对分类变量
;④对分类变量![]() 与
与![]() ,对它们的随机变量
,对它们的随机变量![]() 的观测值
的观测值![]() 来说,
来说,![]() 越小,则“
越小,则“![]() 与
与![]() 有关系”的把握程度越大.其中正确命题的序号是__________.
有关系”的把握程度越大.其中正确命题的序号是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() .
.
(1)若函数![]() 在
在![]() 处取得极值,求实数
处取得极值,求实数![]() 的值;
的值;
(2)在(1)的结论下,若关于![]() 的不等式
的不等式![]() ,当
,当![]() 时恒成立,求
时恒成立,求![]() 的值;
的值;
(3)令![]() ,若关于
,若关于![]() 的方程
的方程![]() 在
在![]() 内至少有两个解,求出实数
内至少有两个解,求出实数![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】深受广大球迷喜爱的某支欧洲足球队.在对球员的使用上总是进行数据分析,为了考察甲球员对球队的贡献,现作如下数据统计:
球队胜 | 球队负 | 总计 | |
甲参加 |
|
|
|
甲未参加 |
|
|
|
总计 |
|
|
|
(1)求![]() 的值,据此能否有
的值,据此能否有![]() 的把握认为球队胜利与甲球员参赛有关;
的把握认为球队胜利与甲球员参赛有关;
(2)根据以往的数据统计,乙球员能够胜任前锋、中锋、后卫以及守门员四个位置,且出场率分别为:![]() ,当出任前锋、中锋、后卫以及守门员时,球队输球的概率依次为:
,当出任前锋、中锋、后卫以及守门员时,球队输球的概率依次为:![]() .则:
.则:
1)当他参加比赛时,求球队某场比赛输球的概率;
2)当他参加比赛时,在球队输了某场比赛的条件下,求乙球员担当前锋的概率;
3)如果你是教练员,应用概率统计有关知识.该如何使用乙球员?
附表及公式:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了鼓励节约用电,辽宁省实行阶梯电价制度,其中每户的用电单价与户年用电量的关系如下表所示.
分档 | 户年用电量(度) | 用电单价(元/度) |
第一阶梯 |
| 0.5 |
第二阶梯 |
| 0.55 |
第三阶梯 |
| 0.80 |
记用户年用电量为![]() 度时应缴纳的电费为
度时应缴纳的电费为![]() 元.
元.
(1)写出![]() 的解析式;
的解析式;
(2)假设居住在沈阳的范伟一家2018年共用电3000度,则范伟一家2018年应缴纳电费多少元?
(3)居住在大连的张莉一家在2018年共缴纳电费1942元,则张莉一家在2018年用了多少度电?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com