
(共14分,6分+8分)
某企业去年的纯利润为500万元,因设备老化等原因,企业的生产能力将逐年下降。若不进行技术改造,预测今年起每年比上一年的纯利润减少20万元。今年初该企业一次性投入资金600万元进行技术改造,预测在未扣除技术改造资金的情况下,第n年(今年为第一年)的利润为500(1+)万元(n为正整数)。设从今年起的前n年,若该企业不进行技术改造的累计纯利润为An万元,进行技术改造后的累计纯利润为Bn万元(需扣除技术改造资金)![]()
(1)、求An、Bn的表达式;(2)、依上述预测,从今年起该企业至少经过多少年,进行技术改造后的累计纯利润超过不进行技术改造的累计纯利润?
23(共10分,每个空格2分)
课本在介绍“i2=-1的几何意义”中讲到:将复平面上的向量乘以i就是沿逆时针方向旋转900,那么乘以-i就是沿顺时针方向旋转900。做以下填空:
已知复平面上的向量![]() 分别对应复数3-i、-2+i,则向量
分别对应复数3-i、-2+i,则向量![]() 对应的复数为 ;那么,以线段MN为一边作两个正方形MNQP和MNQ,P,,则点P、Q对应的复数分别为 、 ;点P,、Q,对应的复数分别为 、 。
对应的复数为 ;那么,以线段MN为一边作两个正方形MNQP和MNQ,P,,则点P、Q对应的复数分别为 、 ;点P,、Q,对应的复数分别为 、 。
(共14分,6分+8分) K^S*5U.
解:①依题意,有An=(500-20)+(500-40)+(500-60)+…+(500-20n)=490n-10n2, Bn=500[(1+)+(1+)+…+(1+)]-600=500n--100
②依题意,考查Bn-An =10[n(n+1)--10],
由于函数y=x(x+1)--10在(0,+∞)上为增函数, K^S*5U.
当n=1或2或3时,n(n+1)--10 <0
当n≥4时,n(n+1)--10≥20--10>0;∴仅当n≥4时,Bn>An
∴至少经过4年,该企业进行技术改造后的累计纯利润超过不进行技术改造的累计纯利润![]()
23.答案:-5+2i;5+4i;6i;1-6i;-4-4i


科目:高中数学 来源: 题型:
(本小题满分12分)
某学校举行知识竞赛,第一轮选拔共设有A、B、C、D四个问题,规则如下:
每位参加者记分器的初始分均为10分,答对问题A、B、C、D分别加1分、2分、3分、6分,答错任一题减2分;
每回答一题,记分器显示累计分数,当累计分数小于8分时,答题结束,淘汰出局;当累计分数大于或等于14分时,答题结束,进入下一轮;当答完四题,累计分数仍不足14分时,答题结束,淘汰出局;
每位参加者按问题A、B、C、D顺序作答,直至答题结束。
假设甲同学对问题A、B、C、D回答正确的概率依次为![]() 、
、![]() 、
、![]() 、
、![]() ,且各题回答正确与否相互之间没有影响。
,且各题回答正确与否相互之间没有影响。
(Ⅰ)求甲同学能进入下一轮的概率;
(Ⅱ)用ξ表示甲同学本轮答题结束时答题的个数,求ξ的分布列和数学期望Εξ。
查看答案和解析>>
科目:高中数学 来源: 题型:
(共14分,6分+8分)
某企业去年的纯利润为500万元,因设备老化等原因,企业的生产能力将逐年下降。若不进行技术改造,预测今年起每年比上一年的纯利润减少20万元。今年初该企业一次性投入资金600万元进行技术改造,预测在未扣除技术改造资金的情况下,第n年(今年为第一年)的利润为500(1+)万元(n为正整数)。设从今年起的前n年,若该企业不进行技术改造的累计纯利润为An万元,进行技术改造后的累计纯利润为Bn万元(需扣除技术改造资金)![]()
(1)、求An、Bn的表达式;(2)、依上述预测,从今年起该企业至少经过多少年,进行技术改造后的累计纯利润超过不进行技术改造的累计纯利润?
23(共10分,每个空格2分)
课本在介绍“i2=-1的几何意义”中讲到:将复平面上的向量乘以i就是沿逆时针方向旋转900,那么乘以-i就是沿顺时针方向旋转900。做以下填空:
已知复平面上的向量![]() 分别对应复数3-i、-2+i,则向量
分别对应复数3-i、-2+i,则向量![]() 对应的复数为 ;那么,以线段MN为一边作两个正方形MNQP和MNQ,P,,则点P、Q对应的复数分别为 、 ;点P,、Q,对应的复数分别为 、 。
对应的复数为 ;那么,以线段MN为一边作两个正方形MNQP和MNQ,P,,则点P、Q对应的复数分别为 、 ;点P,、Q,对应的复数分别为 、 。
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题共14分)国家教育部、体育总局和共青团中央曾共同号召,在全国各级各类学校要广泛、深入地开展全国亿万大中小学生阳光体育运动.为此某网站于2010年1月18日至24日,在全国范围内进行了持续一周的在线调查,随机抽取其中200名大中小学生的调查情况,就每天的睡眠时间分组整理如下表所示:
 (1)估计每天睡眠时间小于8小时的学生所占的百分比约是多少;
(1)估计每天睡眠时间小于8小时的学生所占的百分比约是多少;
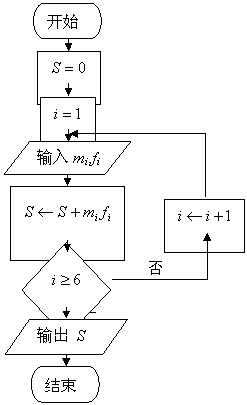
(2)该网站利用如图所示的算法流程图,对样本数据作进一步统计分析,求输出的![]() 的值,并说明
的值,并说明![]() 的统计意义.
的统计意义.
| 序号( | 每天睡眠时间 (小时) | 组中值( | 频数 | 频率 ( |
| 1 | [4,5) | 4.5 | 8 | 0.04 |
| 2 | [5,6) | 5.5 | 52 | 0.26 |
| 3 | [6,7) | 6.5 | 60 | 0.30 |
| 4 | [7,8) | 7.5 | 56 | 0.28 |
| 5 | [8,9) | 8.5 | 20 | 0.10 |
| 6 | [9,10) | 9.5 | 4 | 0.02 |
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分12分)
某学校举行知识竞赛,第一轮选拔共设有A、B、C、D四个问题,规则如下:
每位参加者记分器的初始分均为10分,答对问题A、B、C、D分别加1分、2分、3分、6分,答错任一题减2分;
每回答一题,记分器显示累计分数,当累计分数小于8分时,答题结束,淘汰出局;当累计分数大于或等于14分时,答题结束,进入下一轮;当答完四题,累计分数仍不足14分时,答题结束,淘汰出局;
每位参加者按问题A、B、C、D顺序作答,直至答题结束。
假设甲同学对问题A、B、C、D回答正确的概率依次为![]() 、
、![]() 、
、![]() 、
、![]() ,且各题回答正确与否相互之间没有影响。
,且各题回答正确与否相互之间没有影响。
(Ⅰ)求甲同学能进入下一轮的概率;
(Ⅱ)用ξ表示甲同学本轮答题结束时答题的个数,求ξ的分布列和数学期望Εξ。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com