
【题目】已知函数f(x)=lnx﹣mx(m∈R).
(1)若曲线y=f(x)过点P(1,﹣1),求曲线y=f(x)在点P的切线方程;
(2)若f(x)≤0恒成立求m的取值范围;
(3)求函数f(x)在区间[1,e]上最大值.
【答案】
(1)解:∵f(x)过点P(1,﹣1),
∴﹣1=ln1﹣m,∴m=1,
∴f(x)=lnx﹣x,
![]() ,
,
f'(1)=0,
∴过点P(1,﹣1)的切线方程为y=﹣1
(2)解:∵f(x)≤0恒成立,
即lnx﹣mx≤0恒成立,
∴mx≥lnx,
又∵f(x)定义域为(0,+∞),
∴ ![]() 恒成立;
恒成立;
设 ![]() ,
,
∵ ![]() ,
,
∴当x=e时,g'(e)=0
当0<x<e时,g'(x)>0,g(x)为单调增函数,
当x>e时,g'(x)<0,g(x)为单调减函数,
∴ ![]() ,
,
∴当 ![]() 时,f(x)≤0恒成立
时,f(x)≤0恒成立
(3)解:∵ ![]() ,
,
①当m≤0时,f'(x)>0,
∴f(x)在(0,+∞)为单增函数,
∵在x∈[1,e]上,f(x)max=f(e)=1﹣me;
②当 ![]() ,即
,即 ![]() 时,
时,
当 ![]() 时,f'(x)>0,f(x)为单增函数,
时,f'(x)>0,f(x)为单增函数,
当 ![]() 时,f'(x)<0,f(x)为单减函数,
时,f'(x)<0,f(x)为单减函数,
∴x∈[1,e]上, ![]() ;
;
③当m>1时,即 ![]() 在
在 ![]() 为单减函数,
为单减函数,
∴x∈[1,e]上,f(x)max=f(1)=﹣m;
④当 ![]() ,即
,即 ![]() 时,
时,
f(x)在 ![]() 为单增函数,
为单增函数,
∴x∈[1,e]时,f(x)max=f(e)=1﹣me;
综上所述,
当 ![]() 时,f(x)max=f(e)=1﹣me,
时,f(x)max=f(e)=1﹣me,
当 ![]() 时,
时, ![]()
当m>1时,f(x)max=f(1)=﹣m
【解析】(1)由f(x)过点P(1,﹣1)可得﹣1=ln1﹣m,从而解出m=1,进而求曲线y=f(x)在点P的切线方程;(2)原式可化为lnx﹣mx≤0恒成立,结合x>0可化为 ![]() 恒成立,从而化为求
恒成立,从而化为求 ![]() 的最大值,利用导数求最值;(3)由
的最大值,利用导数求最值;(3)由 ![]() 讨论,m的取值,以确定函数函数f(x)在区间[1,e]上的单调性,从而求函数在区间[1,e]上的最大值.
讨论,m的取值,以确定函数函数f(x)在区间[1,e]上的单调性,从而求函数在区间[1,e]上的最大值.
【考点精析】利用函数的最大(小)值与导数对题目进行判断即可得到答案,需要熟知求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值.
比较,其中最大的是一个最大值,最小的是最小值.


 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源: 题型:
【题目】在等比数列{an}中,a1=1,且a2是a1与a3﹣1的等差中项.
(1)求数列{an}的通项公式;
(2)若数列{bn}满足 ![]() .求数列{bn}的前n项和
.求数列{bn}的前n项和 ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() 是[1,∞]上的增函数.当实数m取最大值时,若存在点Q,使得过Q的直线与曲线y=g(x)围成两个封闭图形,且这两个封闭图形的面积总相等,则点Q的坐标为( )
是[1,∞]上的增函数.当实数m取最大值时,若存在点Q,使得过Q的直线与曲线y=g(x)围成两个封闭图形,且这两个封闭图形的面积总相等,则点Q的坐标为( )
A.(0,﹣3)
B.(0,3)
C.(0,﹣2)
D.(0,2)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,为保护河上古桥OA,规划建一座新桥BC,同时设立一个圆形保护区.规划要求:新桥BC与河岸AB垂直;保护区的边界为圆心M在线段OA上并与BC相切的圆,且古桥两端O和A到该圆上任意一点的距离均不少于80 m.经测量,点A位于点O正北方向60 m处,点C位于点O正东方向170 m处(OC为河岸),tan∠BCO=![]() .
.
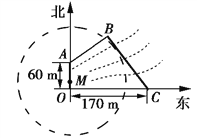
(1)求新桥BC的长;
(2)当OM多长时,圆形保护区的面积最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2x
(1)试求函数F(x)=f(x)+f(2x),x∈(﹣∞,0]的最大值;
(2)若存在x∈(﹣∞,0),使|af(x)﹣f(2x)|>1成立,试求a的取值范围;
(3)当a>0,且x∈[0,15]时,不等式f(x+1)≤f[(2x+a)2]恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下四个命题中:
①某地市高三理科学生有15000名,在一次调研测试中,数学成绩 ![]() 服从正态分布
服从正态分布 ![]() ,已知
,已知 ![]() ,若按成绩分层抽样的方式抽取100份试卷进行分析,则应从120分以上(包括120分)的试卷中抽取
,若按成绩分层抽样的方式抽取100份试卷进行分析,则应从120分以上(包括120分)的试卷中抽取 ![]() 份;
份;
②已知命题 ![]() ,则
,则 ![]() :
: ![]() ;
;
③在 ![]() 上随机取一个数
上随机取一个数 ![]() ,能使函数
,能使函数 ![]() 在
在 ![]() 上有零点的概率为
上有零点的概率为 ![]() ;
;
④设 ![]() ,则“
,则“ ![]() ”是“
”是“ ![]() ”的充要条件.
”的充要条件.
其中真命题的序号为.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(x-a)(x-b)(其中a>b),若f(x)的图象如图所示,则函数g(x)=ax+b的图象大致为( )

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是双曲线
是双曲线![]() 上一点,
上一点, ![]() ,
, ![]() 分别是双曲线左、右两个焦点,若
分别是双曲线左、右两个焦点,若![]() ,则
,则![]() 等于( )
等于( )
A. 1 B. 17 C. 1或17 D. 以上答案均不对
【答案】B
【解析】根据双曲线的定义得到![]() 根据双曲线的焦半径的范围得到
根据双曲线的焦半径的范围得到![]() 故结果为17.
故结果为17.
故答案为:B。
【题型】单选题
【结束】
10
【题目】某中学学生会为了调查爱好游泳运动与性别是否有关,通过随机询问110名性别不同的高中生是否爱好游泳运动得到如下的列联表:由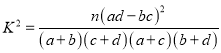 并参照附表,得到的正确结论是( )
并参照附表,得到的正确结论是( )
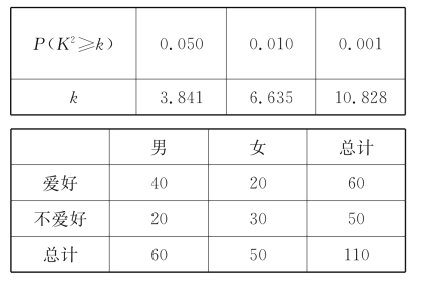
A. 在犯错误的概率不超过![]() 的前提下,认为“爱好游泳运动与性别有关”
的前提下,认为“爱好游泳运动与性别有关”
B. 在犯错误的概率不超过![]() 的前提下,认为“爱好游泳运动与性别无关”
的前提下,认为“爱好游泳运动与性别无关”
C. 有![]() 的把握认为“爱好游泳运动与性别有关”
的把握认为“爱好游泳运动与性别有关”
D. 有![]() 的把握认为“爱好游泳运动与性别无关”
的把握认为“爱好游泳运动与性别无关”
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com