
【题目】已知函数![]() 具有如下性质:在
具有如下性质:在![]() 上是减函数,在
上是减函数,在![]() 上是增函数.
上是增函数.
(1)若函数![]() 的值域为
的值域为![]() ,求b的值;
,求b的值;
(2)已知函数![]() ,
,![]() ,求函数
,求函数![]() 的单调区间和值域;
的单调区间和值域;
(3)对于(2)中的函数![]() 和函数
和函数![]() ,若对任意
,若对任意![]() ,总存在
,总存在![]() ,使得
,使得![]() 成立,求实数c的值.
成立,求实数c的值.
 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案科目:高中数学 来源: 题型:
【题目】如图,一个铝合金窗分为上、下两栏,四周框架和中间隔档的材料为铝合金,宽均为6![]() ,上栏与下栏的框内高度(不含铝合金部分)的比为1:2,此铝合金窗占用的墙面面积为28800
,上栏与下栏的框内高度(不含铝合金部分)的比为1:2,此铝合金窗占用的墙面面积为28800![]() ,设该铝合金窗的宽和高分别为
,设该铝合金窗的宽和高分别为![]() ,铝合金窗的透光部分的面积为
,铝合金窗的透光部分的面积为![]() .
.
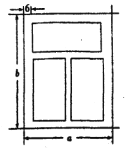
(1)试用![]() 表示
表示![]() ;
;
(2)若要使![]() 最大,则铝合金窗的宽和高分别为多少?
最大,则铝合金窗的宽和高分别为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
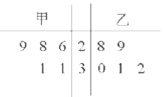
【题目】为比较甲、乙两地某月14时的气温状况,随机选取该月中的5天,将这5天中14时的气温数据(单位:℃)制成如图所示的茎叶图.考虑以下结论:
①甲地该月14时的平均气温低于乙地该月14时的平均气温;
②甲地该月14时的平均气温高于乙地该月14时的平均气温;
③甲地该月14时的平均气温的标准差小于乙地该月14时的气温的标准差;
④甲地该月14时的平均气温的标准差大于乙地该月14时的气温的标准差.
其中根据茎叶图能得到的统计结论的标号为( )
A.①③B.①④C.②③D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率
的离心率![]() ,左、右焦点分别为
,左、右焦点分别为![]() ,点
,点![]() ,点
,点![]() 在线段
在线段![]() 的中垂线上.
的中垂线上.
(1)求椭圆![]() 的方程;
的方程;
(2)设直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,直线
两点,直线![]() 与
与![]() 的倾斜角分别为
的倾斜角分别为![]() ,且
,且![]() ,求证:直线
,求证:直线![]() 过定点,并求该定点的坐标.
过定点,并求该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年“十一”期间,高速公路车辆较多.某调查公司在一服务区从七座以下小型汽车中按进服务区的先后每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查,将他们在某段高速公路的车速(![]() )分成六段:
)分成六段: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,后得到如图的频率分布直方图.
,后得到如图的频率分布直方图.

(1)求这40辆小型车辆车速的众数和中位数的估计值;
(2)若从车速在![]() 的车辆中任抽取2辆,求车速在
的车辆中任抽取2辆,求车速在![]() 的车辆恰有一辆的概率.
的车辆恰有一辆的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区高考实行新方案,规定:语文、数学和英语是考生的必考科目,考生还须从物理、化学、生物、历史、地理和政治六个科目中选取三个科目作为选考科目,若一名学生从六个科目中选出了三个科目作为选考科目,则称该学生的选考方案确定;否则,称该学生选考方案待确定.例如,学生甲选择“物理、化学和生物”三个选考科目,则学生甲的选考方案确定,“物理、化学和生物”为其选考方案.
某学校为了了解高一年级420名学生选考科目的意向,随机选取30名学生进行了一次调查,统计选考科目人数如下表:
性别 | 选考方案确定情况 | 物理 | 化学 | 生物 | 历史 | 地理 | 政治 |
男生 | 选考方案确定的有8人 | 8 | 8 | 4 | 2 | 1 | 1 |
选考方案待确定的有6人 | 4 | 3 | 0 | 1 | 0 | 0 | |
女生 | 选考方案确定的有10人 | 8 | 9 | 6 | 3 | 3 | 1 |
选考方案待确定的有6人 | 5 | 4 | 1 | 0 | 0 | 1 |
(Ⅰ)估计该学校高一年级选考方案确定的学生中选考生物的学生有多少人?
(Ⅱ)假设男生、女生选择选考科目是相互独立的.从选考方案确定的8位男生随机选出1人,从选考方案确定的10位女生中随机选出1人,试求该男生和该女生的选考方案中都含有历史科目的概率;
(Ⅲ)从选考方案确定的8名男生随机选出2名,设随机变量两名男生选考方案相同时![]() ,两名男生选考方案不同时
,两名男生选考方案不同时![]() ,求
,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com