
【题目】如图,△ABC是边长为4的等边三角形,△ABD是等腰直角三角形,AD⊥BD,平面ABC⊥平面ABD,且EC⊥平面ABC,EC=2.
(1)证明:DE∥平面ABC;
(2)证明:AD⊥BE.
【答案】证明:(1)取AB的中点F,连接DF,CF,
∵△ABC是边长为4的等边三角形,△ABD是等腰直角三角形,AD⊥BD,平面ABC⊥平面ABD,
∴DF⊥CF,
∵DF=![]() BC=2
BC=2
又∵EC⊥平面ABC,既有:EC⊥FC,EC=2.
∴DF![]() EC,故四边形DEFC为平行四边形,
EC,故四边形DEFC为平行四边形,
∴DE∥FC
∴DE平面ABC,可得DE∥平面ABC.
(2)以FA,FC,FD为x,y,z轴的正方向建立直角坐标系,
则有:A(2,0,0),D(0,0,2),B(﹣2,0,0),E(0,2![]() ,2)
,2)![]() =(﹣2,0,2),
=(﹣2,0,2),![]() =(﹣2,2
=(﹣2,2![]() ,2)
,2)
由于![]()
![]() =0,
=0,
故AD⊥BE.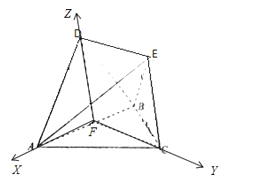
【解析】(1)取AB的中点F,连接DF,CF,由已知可证DF![]() EC,可得四边形DEFC为平行四边形,可得DE∥FC,由DE平面ABC,从而可证DE∥平面ABC.
EC,可得四边形DEFC为平行四边形,可得DE∥FC,由DE平面ABC,从而可证DE∥平面ABC.
(2)以FA,FC,FD为x,y,z轴的正方向建立直角坐标系,求出向量![]() ,
, ![]() 的坐标,由
的坐标,由![]()
![]() =0,即可证明AD⊥BE.
=0,即可证明AD⊥BE.


 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:高中数学 来源: 题型:
【题目】如图所示,在四棱锥S ABCD中,平面SAD⊥平面ABCD.四边形ABCD为正方形,
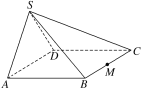
(1)求证:CD⊥平面SAD.
(2)若SA=SD,点M为BC的中点,在棱SC上是否存在点N,使得平面DMN⊥平面ABCD?若存在,请说明其位置,并加以证明;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex·(a+![]() +lnx),其中a∈R.
+lnx),其中a∈R.
(I)若曲线y=f(x)在x=1处的切线与直线y=-![]() 垂直,求a的值;
垂直,求a的值;
(II)当a∈(0,ln2)时,证明:f(x)存在极小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种树苗栽种时高度为A(A为常数)米,栽种n年后的高度记为f(n).经研究发现f(n)近似地满足 f(n)=![]() ,其中
,其中![]() ,a,b为常数,n∈N,f(0)=A.已知栽种3年后该树木的高度为栽种时高度的3倍.
,a,b为常数,n∈N,f(0)=A.已知栽种3年后该树木的高度为栽种时高度的3倍.
(1)栽种多少年后,该树木的高度是栽种时高度的8倍;
(2)该树木在栽种后哪一年的增长高度最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市A,B两所中学的学生组队参加辩论赛,A中学推荐3名男生,2名女生,B中学推荐了3名男生,4名女生,两校推荐的学生一起参加集训,由于集训后队员的水平相当,从参加集训的男生中随机抽取3人,女生中随机抽取3人组成代表队
(1)求A中学至少有1名学生入选代表队的概率.
(2)某场比赛前,从代表队的6名队员中随机抽取4人参赛,设X表示参赛的男生人数,求X得分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在四棱锥![]() 中,底面ABCD是正方形,AC与BD交于点O,
中,底面ABCD是正方形,AC与BD交于点O,![]() 底面ABCD,F为BE的中点,
底面ABCD,F为BE的中点,![]() .
.
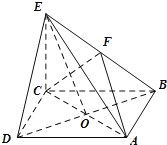
(1)求证:![]() 平面ACF;
平面ACF;
(2)求BE与平面ACE的所成角的正切值;
(3)在线段EO上是否存在点G,使CG![]() 平面BDE ?若存在,求出EG:EO的值,若不存在,请说明理由.
平面BDE ?若存在,求出EG:EO的值,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com