
【题目】(2015秋运城期中)已知函数f(x)=(log2x﹣2)(log4x﹣![]() ).
).
(1)当x∈[1,4]时,求该函数的值域;
(2)若f(x)≤mlog2x对于x∈[4,16]恒成立,求m得取值范围.
【答案】(1)[﹣![]() ,1];(2)m≥
,1];(2)m≥![]() .
.
【解析】
试题(1)利用换元法令t=log2x,t∈[0,2],得f(t)=(t﹣2)(![]() t﹣
t﹣![]() ),利用二次函数性质可得f(0)≥f(t)≥f(
),利用二次函数性质可得f(0)≥f(t)≥f(![]() ),
),
进而求出值域;
(2)由(1)可整理不等式为t+![]() ﹣3≤2m恒成立,只需求出左式的最大值即可,利用构造函数g(t)=t+
﹣3≤2m恒成立,只需求出左式的最大值即可,利用构造函数g(t)=t+![]() ,知在(
,知在(![]() ,+∞)上递增,求出最大值.
,+∞)上递增,求出最大值.
解:令t=log2x,t∈[0,2],
∴f(t)=(t﹣2)(![]() t﹣
t﹣![]() )
)
=![]() (t﹣2)(t﹣1),
(t﹣2)(t﹣1),
∴f(0)≥f(t)≥f(![]() ),
),
∴﹣![]() ≤f(t)≤1,
≤f(t)≤1,
故该函数的值域为[﹣![]() ,1];
,1];
(2)x∈[4,16],
∴t∈[2,4],
∴![]() (t﹣2)(t﹣1)≤mt,
(t﹣2)(t﹣1)≤mt,
∴t+![]() ﹣3≤2m恒成立,
﹣3≤2m恒成立,
令g(t)=t+![]() ,知在(
,知在(![]() ,+∞)上递增,
,+∞)上递增,
∴g(t)≤g(4)=![]() ,
,
∴![]() ﹣3≤2m,
﹣3≤2m,
∴m≥![]() .
.


 优加精卷系列答案
优加精卷系列答案科目:高中数学 来源: 题型:
【题目】甲、乙两名篮球运动员,甲投篮一次命中的概率为![]() ,乙投篮一次命中的概率为
,乙投篮一次命中的概率为![]() ,若甲、乙各投篮三次,设
,若甲、乙各投篮三次,设![]() 为甲、乙投篮命中的次数的差的绝对值,其中甲、乙两人投篮是否命中相互没有影响.
为甲、乙投篮命中的次数的差的绝对值,其中甲、乙两人投篮是否命中相互没有影响.
(1)若甲、乙第一次投篮都命中,求甲获胜(甲投篮命中数比乙多)的概率;
(2)求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三棱锥![]() (如图一)的平面展开图(如图二)中,
(如图一)的平面展开图(如图二)中,![]() 为边长等于
为边长等于![]() 的正方形,△
的正方形,△![]() 和△
和△![]() 均为正三角形,在三棱锥
均为正三角形,在三棱锥![]() 中,
中,

(1)求证:![]() ;
;
(2)求![]() 与平面
与平面![]() 所成的角的大小;
所成的角的大小;
(3)求二面角![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义空间点到几何图形的距离为:这一点到这个几何图形上各点距离中最短距离.
(1)在空间,求与定点![]() 距离等于1的点所围成的几何体的体积和表面积;
距离等于1的点所围成的几何体的体积和表面积;
(2)在空间,线段![]() (包括端点)的长等于1,求到线段
(包括端点)的长等于1,求到线段![]() 的距离等于1的点所围成的几何体的体积和表面积;
的距离等于1的点所围成的几何体的体积和表面积;
(3)在空间,记边长为1的正方形![]() 区域(包括边界及内部的点)为
区域(包括边界及内部的点)为![]() ,求到
,求到![]() 距离等于1的点所围成的几何体的体积和表面积.
距离等于1的点所围成的几何体的体积和表面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
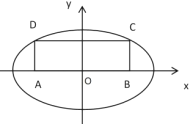
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,以
,以![]() ,
,![]() 为焦点的椭圆
为焦点的椭圆![]() :
:![]() 恰好过
恰好过![]() ,
,![]() 两点.
两点.
(1)求椭圆![]() 的方程;
的方程;
(2)已知![]() 为原点,直线
为原点,直线![]() :
:![]() 与
与![]() 轴交于点
轴交于点![]() ,与椭圆
,与椭圆![]() 相交于
相交于![]() 、
、![]() 两点,且
两点,且![]() 、
、![]() 在
在![]() 轴异侧,若
轴异侧,若![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某生产基地有五台机器,现有五项工作待完成,每台机器完成每项工作后获得的效益值如表所示.若每台机器只完成一项工作,且完成五项工作后获得的效益值总和最大,则下列叙述:①甲只能承担第四项工作;②乙不能承担第二项工作;③丙可以不承担第三项工作;④丁可以承担第三项工作;其中错误的是______.
一 | 二 | 三 | 四 | 五 | |
甲 | 15 | 17 | 14 | 17 | 15 |
乙 | 22 | 23 | 21 | 20 | 20 |
丙 | 9 | 13 | 14 | 12 | 10 |
丁 | 7 | 9 | 11 | 9 | 11 |
戊 | 13 | 15 | 14 | 15 | 11 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com