
【题目】已知函数![]() 的导函数为
的导函数为![]() ,其中a为常数
,其中a为常数
(I)讨论f(x)的单调性;
(Ⅱ)当a=-1时,若不等式![]() 恒成立,求实数m的取值范围
恒成立,求实数m的取值范围
 培优三好生系列答案
培优三好生系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() +
+ ![]() =1(a>b>0)的右焦点为F(1,0),且点P(1,
=1(a>b>0)的右焦点为F(1,0),且点P(1, ![]() )在椭圆C上,O为坐标原点.
)在椭圆C上,O为坐标原点.
(1)求椭圆C的标准方程;
(2)设过定点T(0,2)的直线l与椭圆C交于不同的两点A、B,且∠AOB为锐角,求直线l的斜率k的取值范围;
(3)过椭圆C1: ![]() +
+ ![]() =1上异于其顶点的任一点P,作圆O:x2+y2=
=1上异于其顶点的任一点P,作圆O:x2+y2= ![]() 的两条切线,切点分别为M,N(M,N不在坐标轴上),若直线MN在x轴、y轴上的截距分别为m、n,证明:
的两条切线,切点分别为M,N(M,N不在坐标轴上),若直线MN在x轴、y轴上的截距分别为m、n,证明: ![]() +
+ ![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一装有水的直三棱柱ABC-A1B1C1容器(厚度忽略不计),上下底面均为边长为5的正三角形,侧棱为10,侧面AA1B1B水平放置,如图所示,点D、E、F、G分别在棱CA、CB、C1B1、C1A1上,水面恰好过点D,E,F,C,且CD=2

(1)证明:DE∥AB;
(Ⅱ)若底面ABC水平放置时,求水面的高
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线C1的参数方程为 ![]() (φ为参数,0≤φ≤π),曲线C2的参数方程为
(φ为参数,0≤φ≤π),曲线C2的参数方程为  (t为参数).
(t为参数).
(1)求C1的普通方程并指出它的轨迹;
(2)以O为极点,x轴的非负半轴为极轴建立极坐标系,射线OM:θ= ![]() 与半圆C的交点为O,P,与直线l的交点为Q,求线段PQ的长.
与半圆C的交点为O,P,与直线l的交点为Q,求线段PQ的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() +
+ ![]() =1(α>b>0)的右焦点到直线x﹣y+3
=1(α>b>0)的右焦点到直线x﹣y+3 ![]() =0的距离为5,且椭圆的一个长轴端点与一个短轴端点间的距离为
=0的距离为5,且椭圆的一个长轴端点与一个短轴端点间的距离为 ![]() .
.
(1)求椭圆C的方程;
(2)在x轴上是否存在点Q,使得过Q的直线与椭圆C交于A、B两点,且满足 ![]() +
+ ![]() 为定值?若存在,请求出定值,并求出点Q的坐标;若不存在,请说明理由.
为定值?若存在,请求出定值,并求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为响应十九大报告提出的实施乡村振兴战略,某村庄投资![]() 万元建起了一座绿色农产品加工厂.经营中,第一年支出
万元建起了一座绿色农产品加工厂.经营中,第一年支出![]() 万元,以后每年的支出比上一年增加了
万元,以后每年的支出比上一年增加了![]() 万元,从第一年起每年农场品销售收入为
万元,从第一年起每年农场品销售收入为![]() 万元(前
万元(前![]() 年的纯利润综合=前
年的纯利润综合=前![]() 年的 总收入-前
年的 总收入-前![]() 年的总支出-投资额
年的总支出-投资额![]() 万元).
万元).
(1)该厂从第几年开始盈利?
(2)该厂第几年年平均纯利润达到最大?并求出年平均纯利润的最大值.
【答案】(1) 从第![]() 开始盈利(2) 该厂第
开始盈利(2) 该厂第![]() 年年平均纯利润达到最大,年平均纯利润最大值为
年年平均纯利润达到最大,年平均纯利润最大值为![]() 万元
万元
【解析】试题分析:(1)根据公式得到![]() ,令函数值大于0解得参数范围;(2)根据公式得到
,令函数值大于0解得参数范围;(2)根据公式得到![]() ,由均值不等式得到函数最值.
,由均值不等式得到函数最值.
解析:
由题意可知前![]() 年的纯利润总和
年的纯利润总和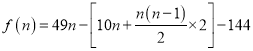
![]()
(1)由![]() ,即
,即![]() ,解得
,解得![]()
由![]() 知,从第
知,从第![]() 开始盈利.
开始盈利.
(2)年平均纯利润![]()
因为![]() ,即
,即![]()
所以![]()
当且仅当![]() ,即
,即![]() 时等号成立.
时等号成立.
年平均纯利润最大值为![]() 万元,
万元,
故该厂第![]() 年年平均纯利润达到最大,年平均纯利润最大值为
年年平均纯利润达到最大,年平均纯利润最大值为![]() 万元.
万元.
【题型】解答题
【结束】
21
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,并且满足
,并且满足![]() ,
, ![]() .
.
(1)求数列![]() 通项公式;
通项公式;
(2)设![]() 为数列
为数列![]() 的前
的前![]() 项和,求证:
项和,求证: ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com