
【题目】设双曲线 ![]() 的两个焦点分别为F1、F2离心率e=2.
的两个焦点分别为F1、F2离心率e=2.
(1)求此双曲线的渐近线l1、l2的方程;
(2)若A、B分别为l1、l2上的点,且 ![]() 求线段AB的中点M的轨迹方程.
求线段AB的中点M的轨迹方程.
(3)过点N(1,0)能否作直线l , 使l与双曲线交于不同两点P、Q.且 ![]() ,若存在,求直线l的方程,若不存在,说明理由.
,若存在,求直线l的方程,若不存在,说明理由.
【答案】
(1)
【解答】双曲线离心率为![]() ,
,![]() ,所以渐近线方程:
,所以渐近线方程: ![]()
(2)
【解答】设A(x1,y1)、B(x2,y2)AB的中点M(x,y)∵2|AB|=5|F1F2|∴|AB|=10
∴(x1,x2)2+(y1–y2)2=100,又 ![]() ,
, ![]() ,x1+x2=2x,y1+y2=2y.
,x1+x2=2x,y1+y2=2y.
∴![]() ,
,![]()
∴![]() , 即
, 即 ![]()
(3)
【解答】假设存在这样的直线e,设其方程为y=k(x-1) P(x1,y1),Q(x2,y2)∵ ![]()
∴x1x2+y1y2=0 ∴x1x2+k2[x1x2-(x1+x2)+1]=0 ①
由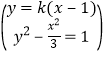 得(3k2-1)x2-6k2x+3k2-3=0 ∴
得(3k2-1)x2-6k2x+3k2-3=0 ∴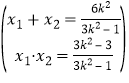 ②
②
由①②得: k2+3=0 ∴k不存在,即这样的直线不存在.
【解析】本题考查了双曲线的定义分析问题、解决问题的能力


科目:高中数学 来源: 题型:
【题目】如图,两个椭圆![]() ,
, ![]() 内部重叠区域的边界记为曲线C,P是曲线C上的任意一点,给出下列四个判断:
内部重叠区域的边界记为曲线C,P是曲线C上的任意一点,给出下列四个判断:
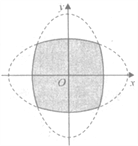
①P到F1(-4,0)、F2(4,0)、E1(0,-4)、E2(0,4)四点的距离之和为定值;
②曲线C关于直线y=x、y=-x均对称;③曲线C所围区域面积必小于36.
④曲线C总长度不大于6π.上述判断中正确命题的序号为________________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】求满足下列各条件的椭圆的标准方程.
(1)长轴长是短轴长的2倍且经过点A(2,0);
(2)短轴一个端点与两焦点组成一个正三角形,且焦点到同侧顶点的距离为.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动点M(x,y)到直线l:x=4的距离是它到点N(1,0)的距离的2倍.
(1)求动点M的轨迹C的方程;
(2)过点P(0,3)的直线m与轨迹C交于A,B两点.若A是PB的中点,求直线m的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆E经过点A(2,3),对称轴为坐标轴,焦点F1 , F2在x轴上,离心率e= ![]() .
. 
(1)求椭圆E的方程;
(2)求∠F1AF2的角平分线所在直线的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com