
【题目】在某单位的职工食堂中,食堂每天以![]() 元/个的价格从面包店购进面包,然后以
元/个的价格从面包店购进面包,然后以![]() 元/个的价格出售.如果当天卖不完,剩下的面包以
元/个的价格出售.如果当天卖不完,剩下的面包以![]() 元/个的价格卖给饲料加工厂.根据以往统计资料,得到食堂每天面包需求量的频率分布直方图如下图所示.食堂某天购进了90个面包,以
元/个的价格卖给饲料加工厂.根据以往统计资料,得到食堂每天面包需求量的频率分布直方图如下图所示.食堂某天购进了90个面包,以![]() (单位:个,
(单位:个, ![]() )表示面包的需求量,
)表示面包的需求量, ![]() (单位:元)表示利润.
(单位:元)表示利润.
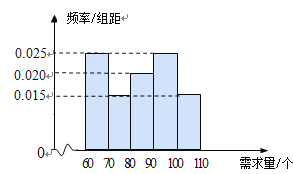
(Ⅰ)求![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(Ⅱ)根据直方图估计利润![]() 不少于
不少于![]() 元的概率;
元的概率;
(III)在直方图的需求量分组中,以各组的区间中点值代表该组的各个值,并以需求量落入该区间的频率作为需求量取该区间中间值的概率(例如:若需求量![]() ,则取
,则取![]() ,且
,且![]() 的概率等于需求量落入
的概率等于需求量落入![]() 的频率),求
的频率),求![]() 的分布列和数学期望.
的分布列和数学期望.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】某校从高一年级随机抽取了![]() 名学生第一学期的数学学期综合成绩和物理学期综合成绩.
名学生第一学期的数学学期综合成绩和物理学期综合成绩.
列表如下:
学生序号 |
|
|
|
|
|
|
|
|
|
|
数学学期综合成绩 |
|
|
|
|
|
|
|
|
|
|
物理学期综合成绩 |
|
|
|
|
|
|
|
|
|
|
学生序号 |
|
|
|
|
|
|
|
|
|
|
数学学期综合成绩 |
|
|
|
|
|
|
|
|
|
|
物理学期综合成绩 |
|
|
|
|
|
|
|
|
|
|
规定:综合成绩不低于![]() 分者为优秀,低于
分者为优秀,低于![]() 分为不优秀.
分为不优秀.
对优秀赋分![]() ,对不优秀赋分
,对不优秀赋分![]() ,从
,从![]() 名学生中随机抽取
名学生中随机抽取![]() 名学生,若用
名学生,若用![]() 表示这
表示这![]() 名学生两科赋分的和,求
名学生两科赋分的和,求![]() 的分布列和数学期望;
的分布列和数学期望;
根据这次抽查数据,列出![]() 列联表,能否在犯错误的概率不超过
列联表,能否在犯错误的概率不超过![]() 的前提下认为物理成绩与数学成绩有关?
的前提下认为物理成绩与数学成绩有关?
附: 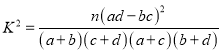 ,其中
,其中![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,曲线![]() 的参数方程为
的参数方程为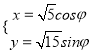 (
(![]() 为参数),直线
为参数),直线![]() 的参数方程为
的参数方程为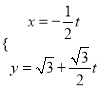 (
(![]() 为参数).以原点为极点,
为参数).以原点为极点, ![]() 轴的正半轴为极轴建立极坐标系,点
轴的正半轴为极轴建立极坐标系,点![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求点![]() 的直角坐标,并求曲线
的直角坐标,并求曲线![]() 的普通方程;
的普通方程;
(2)设直线![]() 与曲线
与曲线![]() 的两个交点为
的两个交点为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业为了对生产的一种新产品进行合理定价,将该产品按事先拟定的价格进行试销,得到以下数据:
单价x(元/件) | 60 | 62 | 64 | 66 | 68 | 70 |
销量y(件) | 91 | 84 | 81 | 75 | 70 | 67 |
(I)画出散点图,并求![]() 关于
关于![]() 的回归方程;
的回归方程;
(II)已知该产品的成本是36元/件,预计在今后的销售中,销量与单价仍然服从(I)中的关系,为使企业获得最大利润,该产品的单价应定为多少元(精确到元)?
附:回归直线![]() 的斜率和截距的最小二乘法估计公式分别为:
的斜率和截距的最小二乘法估计公式分别为:
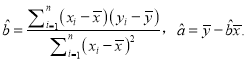
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() 是定义在
是定义在![]() 上的函数,并且满足下面三个条件:①对任意正数
上的函数,并且满足下面三个条件:①对任意正数![]() ,都有
,都有![]() ;②当
;②当![]() 时,
时, ![]() ;③
;③![]() .
.
(1)求![]() ,
, ![]() 的值;
的值;
(2)证明![]() 在
在![]() 上是减函数;
上是减函数;
(3)如果不等式![]() 成立,求
成立,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣2x+2.
(1)求f(x)单调区间
(2)求f(x)在区间[ ![]() ,3]上的最大值和最小值;
,3]上的最大值和最小值;
(3)若g(x)=f(x)﹣mx在[2,4]上是单调函数,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】班主任为了对本班学生的考试成绩进行分析,决定从本班24名女同学,18名男同学中随机抽取一个容量为7的样本进行分析.
(1)如果按照性别比例分层抽样,可得到多少个不同的样本?(写出算式即可,不必计算出结果)
(2)如果随机抽取的7名同学的数学,物理成绩(单位:分)对应如下表:
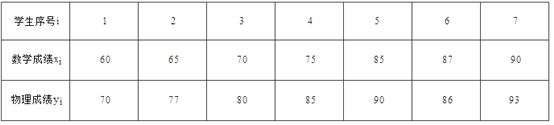
若规定85分以上(包括85分)为优秀,从这7名同学中抽取3名同学,记3名同学中数学和物理成绩均为优秀的人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com